如图,小明用长为3m的竹竿CD做测量工具,测量学校旗杆AB的高度,移动竹竿,使竹竿与旗杆的距离DB=12m,则旗杆AB的高为( )

| A.7 m | B.8 m | C.6m | D.9m |
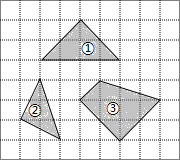
如图,在正方形网格中,每个小正方形的边长均相等.网格中三个多边形(分别标记为①,②,③ 的顶点均在格点上.被一个多边形覆盖的网格线中,竖直部分线段长度之和记为 ,水平部分线段长度之和记为 ,则这三个多边形中满足 的是
| A. |
只有② |
B. |
只有③ |
C. |
②③ |
D. |
①②③ |
如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADE=60°,BD=3,CE=2,则△ABC的边长为( )

| A.9 | B.12 | C.15 | D.18 |
如图,已知D、E分别是△ABC的的AB、AC边上的一点,DE∥BC,且AD: AB=1:2,则△ADE与四边形DBCE的面积之比为( )

A.1:4 B.1:3 C.1:2 D.2:3
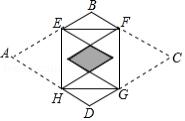
如图,矩形 的四个顶点分别在菱形 的四条边上, .将 , 分别沿边 , 折叠,当重叠部分为菱形且面积是菱形 面积的 时,则 为
A. B.2C. D.4
如图,在Rt△ABC内有边长分别为a、b、c的三个正方形,则a、b、c满足的关系式是( )

A. |
B. |
C. |
D.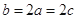 |
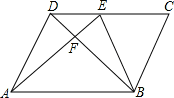
如图,在平行四边形ABCD中,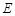 为
为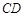 上一点,
上一点,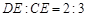 ,连结AE、BD,且
,连结AE、BD,且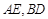 交于点
交于点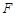 ,则S△DEF:S△ADF:S△ABF等于( )
,则S△DEF:S△ADF:S△ABF等于( )
 B.
B.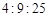 C.
C.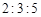 D.
D.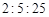
如图,在△ABC中,∠C=90°,D是AC上一点,DE⊥AB于点E,若AC=8,BC=6,DE=3,则AD的长为 ( )

| A.3 | B.4 | C.5 | D.6 |
如图,在△ABC中,∠C=90°,D是AC上的一点,DE⊥AB于点E,若AC=8, BC=6,DE=3,则AD的长为( )

| A.3 | B.4 | C.5 | D.6 |
如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:2,∠OCD=90°,CO=CD.若B(2,0),则点C的坐标为( )
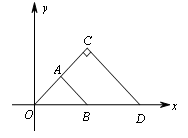
A.(2,2) B.(1,2) C.(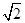 ,2
,2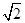 ) D.(2,1)
) D.(2,1)