初中数学相似多边形的性质试题

如图，△ABC中，AB＝8，AC＝6，点D在AC上且AD＝2，如果要在AB上找一点E，使△ADE与△ABC相似，那么AE＝         ．

问题提出
如图①，已知直线l与线段AB平行，试只用直尺作出AB的中点．
初步探索
如图②，在直线l的上方取一个点E，连接EA．EB，分别与l交于点M、N，连接MB．NA，交于点D，再连接ED并延长交AB于点C，则C就是线段AB 的中点．
推理验证
利用图形相似的知识，我们可以推理验证AC=CB．
（1）若线段A．B．C．d长度均不为0，则由下列比例式中，一定可以得出b=d的是
A．      B．      C．       D．
（2）由MN∥AB，可以推出△EFN∽△ECB，△EMN∽△EAB，△MND∽△BAD，△FND∽△CAD．
所以，有，
所以，AC=CB．
拓展研究
如图③，△ABC中，D是BC的中点，点P在AB上．
（3）在图③中只用直尺作直线l∥BC．
（4）求证：l∥BC．

如果，那么下列比例式成立的是（   ）

A．

B．

C．

D．

已知：，则=        ．

如图，在△ABC中，DE∥BC，分别交AB，AC于点D，E．若AD＝1，DB＝2，则△ADE的面积与△ABC的面积的比等于（   ）

A．

B．

C．

D．

兴趣小组的同学要测量树的高度．在阳光下，一名同学测得一根长为1米的竹竿的影长为0．5米，同时另一名同学测量树的高度时，发现树的影子不全落在地面上，有一部分落在教学楼的第一级台阶上，测得此影子长为0．2米，一级台阶高为0．3米，如图所示，若此时落在地面上的影长为4．4米，则树高为（  ）

A．9．5米

B．10．75米

C．11．8米

D．9．8米

两个相似三角形的面积比为4：9，那么它们对应中线的比为        ．

如图，电灯P在横杆AB的正上方，AB在灯光下的影子为CD，AB∥CD，AB＝2m，CD＝5m，点P到CD的距离是3m，则P到AB的距离是（    ）

A．m

B．m

C．m

D．m

若，则=（    ）

A．

B．

C．

D．

下列条件能判断△ABC与△DEF相似的有（   ）
（1）∠A=∠D，∠E=∠C；
（2）；
（3）
（4）；
（5）∠A=∠D，

A．2个

B．3个

C．4个

D．5个

如图：为了测量某棵树的高度，小刚用长为2m的竹竿做测量工具，移动竹竿，使竹竿、树的顶端的影子恰好落在地面的同一点，此时，竹竿与这一点距离6m，与树相距15m，那么这棵的高度为（ ）

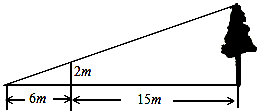
A．5米

B．7米

C．7．5米

D．21米

如图，已知AB、CD、EF都与BD垂直，垂足分别是B、D、F，且AB＝1，CD＝3，那么EF的长是 （   ）

A．    B．   C．    D．

下列说法中正确的是（    ）

A．两个直角三角形相似	B．两个等腰三角形相似
C．两个等边三角形相似	D．两个锐角三角形相似

两个相似等腰直角三角形的面积比是4：1，则它们的周长比是（   ）

A．4：1

B．2：1

C．8：1

D．16：1

下列四组线段中，不构成比例线段的一组是（    ）

A．1 cm，2 cm，3 cm，6 cm

B．2 cm，3 cm，4 cm，6 cm

C．1cm，cm，cm，cm

D．1 cm，2 cm，3 cm，4 cm