如图,一次函数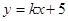 (
( 为常数,且
为常数,且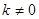 )的图像与反比例函数
)的图像与反比例函数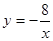 的图像交于
的图像交于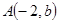 ,
, 两点.
两点.
(1)求一次函数的表达式;
(2)若将直线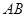 向下平移
向下平移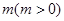 个单位长度后与反比例函数的图像有且只有一个公共点,求
个单位长度后与反比例函数的图像有且只有一个公共点,求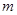 的值.
的值.
反比例函数y=﹣ 的图象上有两点P1(x1,y1),P2(x2,y2),若x1<0<x2,则下列结论正确的是().
的图象上有两点P1(x1,y1),P2(x2,y2),若x1<0<x2,则下列结论正确的是().
| A.y1<y2<0 | B.y1<0<y2 | C.y1>y2>0 | D.y1>0>y2 |
在反比例函数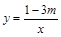 图象上有两点A(x1,y1)、B(x2,y2),x1<0<x2,y1<y2,则m的取值范围是()
图象上有两点A(x1,y1)、B(x2,y2),x1<0<x2,y1<y2,则m的取值范围是()
A.m> |
B.m< |
C.m≥ |
D.m≤ |
抛物线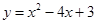 与x轴交于A、B两点(点A在点B的左侧),点C是此抛物线的顶点.
与x轴交于A、B两点(点A在点B的左侧),点C是此抛物线的顶点.
(1)求点A、B、C的坐标;
(2)点C在反比例函数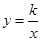 (
(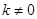 )的图象上,求反比例函数的解析式.
)的图象上,求反比例函数的解析式.
点A(a,1)、B(﹣1,b)都在双曲线y=﹣ 上,点P、Q分别是x轴、y轴上的动点,当四边形PABQ的周长取最小值时,PQ所在直线的解析式是()
上,点P、Q分别是x轴、y轴上的动点,当四边形PABQ的周长取最小值时,PQ所在直线的解析式是()
| A.y=x | B.y=x+1 | C.y=x+2 | D.y=x+3 |
在平面直角坐标系中,我们不妨把纵坐标是横坐标的2倍的点称之为“理想点”,例如点(﹣2,﹣4),(1,2),(3,6)…都是“理想点”,显然这样的“理想点”有有无数多个.
(1)若点M(2,a)是反比例函数 (k为常数,
(k为常数, )图象上的“理想点”,求这个反比例函数的表达式;
)图象上的“理想点”,求这个反比例函数的表达式;
(2)函数 (m为常数,
(m为常数, )的图象上存在“理想点”吗?若存在,请求出“理想点”的坐标;若不存在,请说明理由.
)的图象上存在“理想点”吗?若存在,请求出“理想点”的坐标;若不存在,请说明理由.
反比例函数 的图象经过点
的图象经过点 ,则函数的解析式为____________.
,则函数的解析式为____________.
在复习《反比例函数》一课时,同桌的小明和小芳有一个问题观点不一致.小明认为如果两次分别从1~6六个整数中任取一个数,第一个数作为点P(m,n)的横坐标,第二个数作为点P(m,n)的纵坐标,则点P(m,n)在反比例函数y=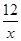 的图象上的概率一定大于在反比例函数y=
的图象上的概率一定大于在反比例函数y=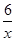 的图象上的概率,而小芳却认为两者的概率相同.你赞成谁的观点?
的图象上的概率,而小芳却认为两者的概率相同.你赞成谁的观点?
(1)试用列表或画树状图的方法列举出所有点P(m,n)的情形;
(2)分别求出点P(m,n)在两个反比例函数的图象上的概率,并说明谁的观点正确.
对于反比例函数y=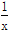 ,下列说法正确的是()
,下列说法正确的是()
| A.图象经过点(1,-1) |
| B.图象位于第二、四象限 |
| C.图象是中心对称图形 |
| D.当x<0时,y随x的增大而增大 |
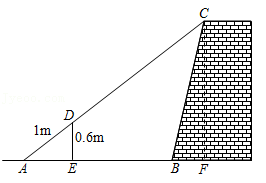
如图,为了测量山坡的护坡石坝高,把一根长为 的竹竿 斜靠在石坝旁,量出竿上 长为 时,它离地面的高度 为 ,则坝高 为 .
当x>0时,函数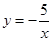 的图象在()
的图象在()
| A.第四象限 | B.第三象限 | C.第二象限 | D.第一象限 |
已知反比例函数y= 的图像经过点P(-1,2),则这个函数图像位于()
的图像经过点P(-1,2),则这个函数图像位于()
| A.第二、三象限 | B.第一、三象限 |
| C.第三、四象限 | D.第二、四象限 |
正比例函数y=2x与反比例函数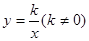 的图象有一个交点为(2,4),则另一个交点坐标为()
的图象有一个交点为(2,4),则另一个交点坐标为()
A.(2,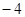 ) ) |
B.(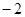 , ,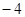 ) ) |
C.(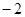 ,4) ,4) |
D.(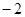 , ,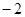 ) ) |