如图,直线l过点A(a,0)和点B(0,b)(其中a>0,b>0).反比例函数y=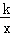 (k>0)的图象与直线l交于C、D两点,连接OC、OD.
(k>0)的图象与直线l交于C、D两点,连接OC、OD.
(1)若a+b=10,△AOB的面积为S,问:当b为何值时,S取最大值?并求出这个最大值;
(2)当S取最大值时,若C,D恰好是线段AB的三等分点,求k的值.
如图,正比例函数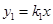 的图象与反比例函数
的图象与反比例函数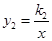 的图象相交于A,B两点,其中点A的横坐标为2,当
的图象相交于A,B两点,其中点A的横坐标为2,当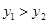 时,x的取值范围是()
时,x的取值范围是()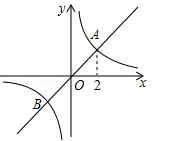
| A.x<﹣2或x>2 |
| B.x<﹣2或0<x<2 |
| C.﹣2<x<0或0<x<﹣2 |
| D.﹣2<x<0或x>2 |
如图,反比例反数y= 与正比例函数y=k2x的图象交于A(﹣2,4),B两点,若
与正比例函数y=k2x的图象交于A(﹣2,4),B两点,若 >k2x,则x的取值范围是().
>k2x,则x的取值范围是().
| A.﹣2<x<0 |
| B.﹣2<x<2 |
| C.﹣2<x<0或x>2 |
| D.x<﹣2或0<x<2 |
近视眼镜的度数 (度)与镜片焦距
(度)与镜片焦距 (米)成反比例,已知400度近视眼镜镜片的焦距为0.25米,则眼镜度数
(米)成反比例,已知400度近视眼镜镜片的焦距为0.25米,则眼镜度数 与镜片焦距
与镜片焦距 之间的函数关系式为 .
之间的函数关系式为 .
如图,已知直线y=2x分别与双曲线y= ,y=
,y= (x>0)交于P、Q两点,且OP=2OQ,点A是双曲线y=
(x>0)交于P、Q两点,且OP=2OQ,点A是双曲线y= 上的动点,过A作AB∥x轴,AC∥y轴,分别交双曲线y=
上的动点,过A作AB∥x轴,AC∥y轴,分别交双曲线y= (x>0)于点B、C.连接BC.
(x>0)于点B、C.连接BC.
(1)求k的值;
(2)随着点A的运动,△ABC的面积是否发生变化?若不变,求出△ABC的面积,若改变,请说明理由.
(3)直线y=2x上是否存在点D,使得点A、B、C、D为顶点的四边平行四边形?若能,求出相应点A的坐标;若不能,请说明理由.
已知△ABC三个顶点A(1,m),B(4,n),C(4,4),直线l过A、B两点,其解析式为y=-x+b.
(1)若双曲线y= (x>0)过点A、B两点,则关于x的方程x2-bx+k=0的解为 ;
(x>0)过点A、B两点,则关于x的方程x2-bx+k=0的解为 ;
(2)当b=5,若双曲线y= (x>0)与△ABC有公共点,求k1的取值范围.
(x>0)与△ABC有公共点,求k1的取值范围.
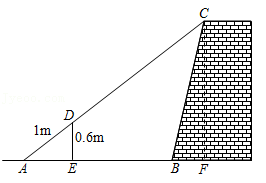
如图,为了测量山坡的护坡石坝高,把一根长为 的竹竿 斜靠在石坝旁,量出竿上 长为 时,它离地面的高度 为 ,则坝高 为 .
当x>0时,函数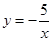 的图象在()
的图象在()
| A.第四象限 | B.第三象限 | C.第二象限 | D.第一象限 |
已知反比例函数y= 的图像经过点P(-1,2),则这个函数图像位于()
的图像经过点P(-1,2),则这个函数图像位于()
| A.第二、三象限 | B.第一、三象限 |
| C.第三、四象限 | D.第二、四象限 |
正比例函数y=2x与反比例函数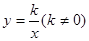 的图象有一个交点为(2,4),则另一个交点坐标为()
的图象有一个交点为(2,4),则另一个交点坐标为()
A.(2,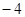 ) ) |
B.(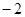 , ,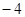 ) ) |
C.(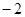 ,4) ,4) |
D.(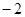 , ,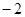 ) ) |