山东省威海市乳山市八年级下学期期末数学试卷
下列说法错误的是( ).
| A.两个等边三角形一定相似 |
| B.两个等腰三角形一定相似 |
| C.两个等腰直角三角形一定相似 |
| D.两个全等三角形一定相似 |
若x=1是一元二次方程(x+1)2﹣a(x+1)﹣2=0的一个根,则a的值是( ).
| A.﹣2 | B.﹣1 | C.1 | D.2 |
若函数y= (k≠0)的图象过点(
(k≠0)的图象过点( ,
, ),则此函数图象位于( ).
),则此函数图象位于( ).
| A.第一、二象限 | B.第一、三象限 |
| C.第二、三象限 | D.第二、四象限 |
x1、x2是一元二次方程3(x﹣1)2=15的两个解,且x1<x2,下列说法正确的是( ).
| A.x1小于﹣1,x2大于3 |
| B.x1小于﹣2,x2大于3 |
| C.x1,x2在﹣1和3之间 |
| D.x1,x2都小于3 |
如图,AD平分∠BAC,AC2=BC•CD,∠C=105°,则∠B=( ).

| A.25° | B.30° | C.35° | D.40° |
反比例函数y= 的图象如图所示,点M是该函数图象上一点,MN垂直于x轴,垂足是点N,如果S△MON=2,则k的值为( ).
的图象如图所示,点M是该函数图象上一点,MN垂直于x轴,垂足是点N,如果S△MON=2,则k的值为( ).

| A.2 | B.﹣2 | C.4 | D.﹣4 |
如图,反比例反数y= 与正比例函数y=k2x的图象交于A(﹣2,4),B两点,若
与正比例函数y=k2x的图象交于A(﹣2,4),B两点,若 >k2x,则x的取值范围是( ).
>k2x,则x的取值范围是( ).

| A.﹣2<x<0 |
| B.﹣2<x<2 |
| C.﹣2<x<0或x>2 |
| D.x<﹣2或0<x<2 |
已知m2﹣m﹣3=0, ﹣
﹣ ﹣3=0,m,n为实数,且m≠
﹣3=0,m,n为实数,且m≠ ,则m•
,则m• 的值为( ).
的值为( ).
| A.﹣3 | B.﹣1 | C.3 | D.1 |
如图,在△ABC中,∠ACB=90°,AC=BC,点F在AB上,连接CF,AE⊥CF于E,BD垂直CF的延长线于点D.若AE=4cm,BD=2cm,则EF的长是( ).

A. cm B.
cm B. cm C.1cm D.
cm C.1cm D. cm
cm
函数y= (k为常数)的图象过点(﹣2,y1)和(﹣
(k为常数)的图象过点(﹣2,y1)和(﹣ ,y2),则y1,y2的大小关系是(填“>”,“=”,“<”) .
,y2),则y1,y2的大小关系是(填“>”,“=”,“<”) .
五边形ABCDE与五边形A1B1C1D1E1A是位似图形,它们在位似中心的同侧,其面积比为9:16,若位似中心O到A的距离为3,则A到A1的距离为 .
如图,一块矩形铁皮的长是宽的2倍,将这个铁皮的四角各剪去一个边长为3cm的小正方形,做成一个无盖的盒子,若盒子的容积是240cm3,则原铁皮的宽为 cm.

如图,在矩形ABCD中,AB=6,BC=8,将矩形ABCD沿对角线AC对折,然后放在桌面上,折叠后所成的图形覆盖的面积(阴影部分的面积)是 .

小明家的玉米产量从2012年的5吨增加到2014年的6.05吨,平均每年增长的百分率是多少?
如图,点A在双曲线y= (x>0)上,过点A作AC⊥x轴,垂足为C,线段OA的垂直平分线BD交x轴于点B,△ABC的周长为4,求点A的坐标.
(x>0)上,过点A作AC⊥x轴,垂足为C,线段OA的垂直平分线BD交x轴于点B,△ABC的周长为4,求点A的坐标.
在如图的方格中,△OAB的顶点坐标分别为O(0,0)、A(﹣2,﹣1)、B(﹣1,﹣3),△O1A1B1与△OAB是关于点P为位似中心的位似图形.
(1)在图中标出位似中心P的位置,并写出点的坐标及△O1A1B1与△OAB的相似比;
(2)以原点O为位似中心,在y轴的左侧画出△OAB的一个位似△OA2B2,使它与△OAB的位似比为2:1,并写出点B的对应点B2的坐标;
(3)在(2)条件下,若点M(a,b)是△OAB边上一点(不与顶点重合),写出M在△OA2B2中的对应点M2的坐标.
如图,点A,D在反比例函数y= (x>0)的图象上,点A的坐标是(2,4),接AD,过点A作AB⊥AD,交y轴于点B,过点D作DC⊥AD,交x轴于点C,连接BC,四边形ABCD为正方形.
(x>0)的图象上,点A的坐标是(2,4),接AD,过点A作AB⊥AD,交y轴于点B,过点D作DC⊥AD,交x轴于点C,连接BC,四边形ABCD为正方形.
(1)求点C的坐标;
(2)求点D的坐标.
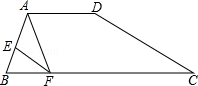
如图,在四边形ABCD中,AB=AD,AC与BD相交于点E,∠ADB=∠ACB.
(1)求证:AD2=AE•AC;
(2)若AB⊥AC,CE=2AE,F是BC的中点,连接AF,判断△ABF的形状,并说明理由.
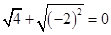
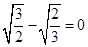

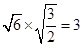
 和
和

 和
和
 和
和
 =( ).
=( ).



 的最小值是 .
的最小值是 . ﹣1)2﹣(
﹣1)2﹣( +
+ )(
)( ).
).
 粤公网安备 44130202000953号
粤公网安备 44130202000953号