平面直角坐标系中,点A的坐标为(4,3),将线段OA绕原点O顺时针旋转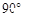 得到
得到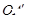 ,则点
,则点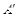 的坐标是
的坐标是
A.( ,3) ,3) |
B.( ,4) ,4) |
C.(3, ) ) |
D.(4, ) ) |
在平面直角坐标系中,点P(2,3)在
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
如图,平面直角坐标系中有一直角梯形OMNH,点H的坐标为(-8,0),点N的坐标为(-6,-4).
(1)画出直角梯形OMNH绕点O旋转180°的图形OABC,并写出顶点A,B,C的坐标(点M的对应点为A, 点N的对应点为B, 点H的对应点为C);
(2)求出过A,B,C三点的抛物线的表达式;
(3)截取CE=OF=AG=m,且E,F,G分别在线段CO,OA,AB上,求四边形BEFG的面积S与m之间的函数关系式,并写出自变量m的取值范围;面积S是否存在最小值?若存在,请求出这个最小值;若不存在,请说明理由;
(4)在(3)的情况下,四边形BEFG是否存在邻边相等的情况,若存在,请直接写出此时m的值,并指出相等的邻边;若不存在,说明理由.
如图,在平面直角坐标系中,以O(0,0),A(1,1),B(3,0)为顶点,构造平行四边形,下列各点中不能作为平行四边形顶点坐标的是()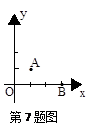
| A.(-3,1) | B.(4,1) | C.(-2,1) | D.(2,-1) |
如图,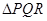 是
是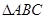 经过某种变换后得到的图形.
经过某种变换后得到的图形.
如果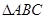 中任意一点
中任意一点 的坐标为(
的坐标为(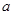 ,
, ),它的对应点
),它的对应点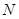 的坐标为.
的坐标为.
在一次夏令营活动中,小霞同学从营地 点出发,要到距离
点出发,要到距离 点
点
 的
的 地去,先沿北偏东
地去,先沿北偏东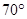 方向到达
方向到达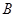 地,然后再沿北偏西
地,然后再沿北偏西 方向走了
方向走了
 到达目的地
到达目的地 ,此时小霞在营地
,此时小霞在营地 的
的
A.北偏东 方向上 方向上 |
B.北偏东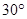 方向上 方向上 |
C.北偏东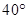 方向上 方向上 |
D.北偏西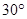 方向上 方向上 |
在平面直角坐标系中,以点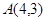 、
、 、
、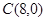 为顶点的三角形向上平移3个单位,得到△
为顶点的三角形向上平移3个单位,得到△ (点
(点 分别为点
分别为点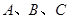 的对应点),然后以点
的对应点),然后以点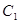 为中心将△
为中心将△ 顺时针旋转
顺时针旋转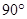 ,得到△
,得到△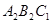 (点
(点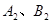 分别是点
分别是点 的对应点),则点
的对应点),则点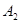 的坐标是 .
的坐标是 .
类比学习:
一动点沿着数轴向右平移3个单位,再向左平移2个单位,相当于向右平移1个单位.用实数加法表示为 3+( )=1.
)=1.
若坐标平面上的点作如下平移:沿x轴方向平移的数量为a(向右为正,向左为负,平移 个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移
个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移 个单位),则把有序数对{a,b}叫做这一平移的“平移量”;“平移量”{a,b}与“平移量”{c,d}的加法运算法则为
个单位),则把有序数对{a,b}叫做这一平移的“平移量”;“平移量”{a,b}与“平移量”{c,d}的加法运算法则为 .
.
解决问题:
(1)计算:{3,1}+{1,2};{1,2}+{3,1}.
(2)①动点P从坐标原点O出发,先按照“平移量”{3,1}平移到A,再按照“平移量”
{1,2}平移到B;若先把动点P按照“平移量”{1,2}平移到C,再按照“平移量”
{3,1}平移,最后的位置还是点B吗? 在图1中画出四边形OABC.
②证明四边形OABC是平行四边形.
(3)如图2,一艘船从码头O出发,先航行到湖心岛码头P(2,3),再从码头P航行到码头Q(5,5),最后回到出发点O. 请用“平移量”加法算式表示它的航行过程.
如图,点Q在直线y=-x上运动,点A的坐标为(1,0),
当线段AQ最短时,点Q的坐标为__________________。
图(五)数在线的A、B、C三点所表示的数分别为a、b、c。根据图中各点位置,判断下列各式何者正确? 
| A.(a-1)(b-1)>0 | B.(b-1)(c-1)>0 | C.(a+1)(b+1)<0 | D.(b+1)(c+1)<0 |
坐标半面上,在第二象限内有一点P,且P点到x轴的距离是4,到y轴的距离是5,则P点坐标为何?
| A.(-5,4) | B.(-4,5) | C.(4,5) | D.(5,-4) |
如图,若A是实数a在数轴上对应的点,则关于a,-a,1的大小关系表示正确的是( ▲)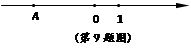
| A.a<1<-a | B.a<-a<1 | C.1<-a<a | D.-a<a<1 |
在平面直角坐标系中,点P(-1,3)位于( ▲)
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
在平面直角坐标系中,线段AB的端点A的坐标为(-3,2),将其先向右平移4个单位,再向下平移3个单位,得到线段A′B′,则点A对应点A′的坐标为.