在平面直角坐标系中,点 与点
与点 关于原点对称,则
关于原点对称,则 的值为( )
的值为( )
| A.33 | B. |
C. |
D.7 |
如图,将正方形OABC放在平面直角坐标系中,O是原点,A的坐标为(1, ),则点C的坐标为( )
),则点C的坐标为( )

A.(﹣ ,1) ,1) |
B.(﹣1, ) ) |
C.( ,1) ,1) |
D.(﹣ ,﹣1) ,﹣1) |
在平面直角坐标系中,点 A的坐标为(1, ),以原点 O为中心,将点 A顺时针旋转60°得到点 A',则点 A′的坐标为( )
| A. |
(0, ) |
B. |
(1,﹣ ) |
C. |
(﹣1, ) |
D. |
(2,0) |
在平面直角坐标系中,孔明做走棋的游戏,其走法是:棋子从原点出发,第1步向右走1个单位,第2步向右走2个单位,第3步向上走1个单位,第4步向右走1个单位…依此类推,第n步的走法是:当n能被3整除时,则向上走1个单位;当n被3除,余数为1时,则向右走1个单位;当n被3除,余数为2时,则向右走2个单位,当走完第100步时,棋子所处位置的坐标是( )
| A.(66,34) | B.(67,33) |
| C.(100,33) | D.(99,34) |
如图,△ABC的三个顶点都在方格纸的格点上,其中点A的坐标是(﹣1,0).现将△ABC绕点A顺时针旋转90°,则旋转后点C的坐标是
| A.(2,1) | B.(1,2) | C.(-2,-1) | D.(-2,1) |
甲乙两位同学用围棋子做游戏.如图所示.现轮到黑棋下子,黑棋下一子后白棋再下一子,使黑棋的5个棋子组成轴对称图形,白棋的5个棋子也组成轴对称图形.则下列下子方法正确的是[说明:棋子的位置用数对表示,如A点在(6,3)]( )

| A.黑(3,7);白(3,5) | B.黑(4,7);白(6,2) |
| C.黑(3,7);白(5,3) | D.黑(4,7);白(2,6) |
如图,将线段 绕点 按顺时针方向旋转 ,得到线段 ,其中点 、 的对应点分别是点 、 ,则点 的坐标是

A. B. C. D.
在平面直角坐标系中,点P(﹣2,3)关于x轴的对称点的坐标是( )
| A.(2,3) | B.(2,﹣3) | C.(﹣2,﹣3) | D.(﹣3,2) |
在平面直角坐标系中,点(3,﹣2)关于y轴对称的点的坐标是( )
| A.(3,2) | B.(3,﹣2) | C.(﹣3,2) | D.(﹣3,﹣2) |
在平面直角坐标系中,等边 如图放置,点 的坐标为 ,每一次将 绕着点 逆时针方向旋转 ,同时每边扩大为原来的2倍,第一次旋转后得到△ ,第二次旋转后得到△ , ,依次类推,则点 的坐标为
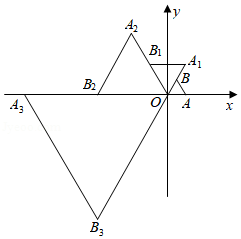
| A. |
, |
B. |
, |
| C. |
, |
D. |
, |
如图,一次函数 的图象与 轴、 轴分别交于点 , ,把直线 绕点 顺时针旋转 交 轴于点 ,则线段 长为
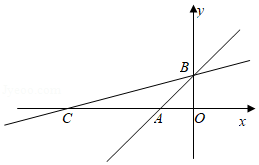
| A. |
|
B. |
|
C. |
|
D. |
|
如图,在平面直角坐标系 中, , , , 是 的内心,将 绕原点逆时针旋转 后, 的对应点 的坐标为
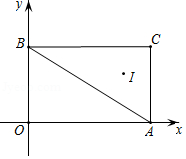
A. B. C. D.
如图,在平面直角坐标系中, 的顶点都在方格线的格点上,将 绕点 顺时针方向旋转 ,得到△ ,则点 的坐标为

A. B. C. D.
如图,在平面直角坐标系中, 是直线 上的一个动点,将 绕点 顺时针旋转 ,得到点 ,连接 ,则 的最小值为

| A. |
|
B. |
|
C. |
|
D. |
|
如图,动点P从(0,3)出发,沿所示方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,当点P第2013次碰到矩形的边时,点P的坐标为( )
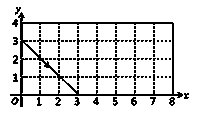
| A.(1,4) | B.(5,0) | C.(6,4) | D.(8,3) |