将一副三角板如图放置在平面直角坐标系中,顶点 与原点 重合, 在 轴正半轴上,且 ,点 在 上, ,将这副三角板整体向右平移 个单位, , 两点同时落在反比例函数 的图象上.

在平面直角坐标系中,平行四边形 的对称中心是坐标原点,顶点 、 的坐标分别是 、 ,将平行四边形 沿 轴向右平移3个单位长度,则顶点 的对应点 的坐标是 .
如图,在平面直角坐标系中,等腰直角三角形 的斜边 在 轴上, ,点 在第一象限.标记点 的位置后,将 沿 轴正方向平移至△ 的位置,使 经过点 ,再标记点 的位置,继续平移至△ 的位置,使 经过点 ,此时点 的坐标为 .

如图,在平面直角坐标系中,已知 , , ,将 先向右平移3个单位长度得到△ ,再绕 顺时针方向旋转 得到△ ,则 的坐标是 .

如图,在平面直角坐标系中,将点 向右平移2个单位长度得到点 ,则点 关于 轴的对称点 的坐标是 .

在平面直角坐标系中,将点 先向右平移2个单位长度,再向上平移3个单位长度,则所得点的坐标是 .
在平面直角坐标系中, 点 的坐标是 ,作点 关于 轴的对称点, 得到点 ,再将点 向下平移 4 个单位, 得到点 ,则点 的坐标是 , .
定义:在平面直角坐标系中,一个图形先向右平移 个单位,再绕原点按顺时针方向旋转 角度,这样的图形运动叫作图形的 变换.
如图,等边 的边长为1,点 在第一象限,点 与原点 重合,点 在 轴的正半轴上.△ 就是 经 变换后所得的图形.
若 经 变换后得△ ,△ 经 变换后得△ ,△ 经 变换后得△ ,依此类推
△ 经 变换后得△ ,则点 的坐标是 ,点 的坐标是 .
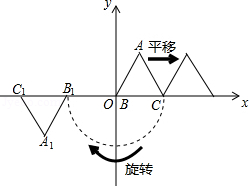
如图,把 经过一定的变换得到△ ,如果 上任意一点 的坐标为 ,那么点 在△ 中的对应点 的坐标为 .

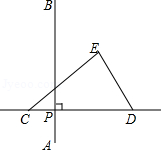
如图,在平面内,线段 , 为线段 上的动点,三角形纸片 的边 所在的直线与线段 垂直相交于点 ,且满足 .若点 沿 方向从点 运动到点 ,则点 运动的路径长为 .
如图,直线 与 轴交于点 ,以 为斜边在 轴上方作等腰直角三角形 ,将 沿 轴向右平移,当点 落在直线 上时,则 平移的距离是 .

如图, 为坐标原点, 是等腰直角三角形, ,点 的坐标为 , ,将该三角形沿 轴向右平移得到 △ ,此时点 的坐标为 , ,则线段 在平移过程中扫过部分的图形面积为 .
