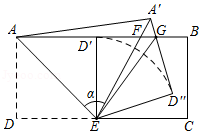
如图,在矩形 中, , .把 沿 折叠,使点 恰好落在 边上的 处,再将 绕点 顺时针旋转 ,得到△ ,使得 恰好经过 的中点 . 交 于点 ,连接 .有如下结论:① 的长度是 ;②弧 的长度是 ;③△ △ ;④△ .上述结论中,所有正确的序号是 .
如图,在 中, , ,将 绕点 按顺时针方向旋转到△ 的位置,点 刚好落在 的延长线上,求点 从开始到结束所经过的路径长为(结果保留 .

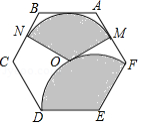
如图,点 为正六边形 的中心,点 为 中点,以点 为圆心,以 的长为半径画弧得到扇形 ,点 在 上;以点 为圆心,以 的长为半径画弧得到扇形 ,把扇形 的两条半径 , 重合,围成圆锥,将此圆锥的底面半径记为 ;将扇形 以同样方法围成的圆锥的底面半径记为 ,则 .
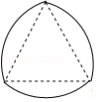
如图,分别以等边三角形的每个顶点为圆心、以边长为半径,在另两个顶点间作一段圆弧,三段圆弧围成的曲边三角形称为勒洛三角形.若等边三角形的边长为 ,则勒洛三角形的周长为 .
如图,在圆心角为90°的扇形 OAB中, OB=2, P为 上任意一点,过点 P作 PE⊥ OB于点 E,设 M为△ OPE的内心,当点 P从点 A运动到点 B时,则内心 M所经过的路径长为 .

抖空竹在我国有着悠久的历史,是国家级的非物质文化遗产之一.如图, , 分别与 相切于点 , ,延长 , 交于点 .若 , 的半径为 ,则图中 的长为 .(结果保留

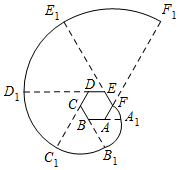
如图,六边形 是正六边形,曲线 叫做“正六边形的渐开线”, , , , , , , 的圆心依次按 , , , , , 循环,且每段弧所对的圆心角均为正六边形的一个外角.当 时,曲线 的长度是 .
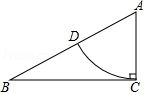
如图,在△ABC中,∠ACB=90°,AC=1,AB=2,以点A为圆心、AC的长为半径画弧,交AB边于点D,则弧CD的长等于 .(结果保留π)
如图,在扇形 中, , 平分 交 于点 ,点 为半径 上一动点.若 ,则阴影部分周长的最小值为 .
