初中数学弧长的计算填空题

将 $\mathit{\Delta ABC}$以 $B$为旋转中心，顺时针旋转 $90°$．得到 $\mathit{\Delta DBE}$， $\mathit{AB}=4$，则点 $A$经过的路径长为　　．

如图，正六边形ABCDEF内接于半径为3的圆O，则劣弧AB的长度为　　．

如图，扇形OAB的圆心角为120°，半径为3，则该扇形的弧长为　　．（结果保留π）

在半径为6cm的圆中，120°的圆心角所对的弧长为　   　cm．

已知扇形的半径为6cm，面积为10πcm²，则该扇形的弧长等于　　．

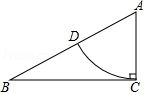
如图，在△ABC中，∠ACB＝90°，AC＝1，AB＝2，以点A为圆心、AC的长为半径画弧，交AB边于点D，则弧CD的长等于　　．（结果保留π）

如图，在圆心角为90°的扇形 OAB中， OB＝2， P为 $\stackrel{⏜}{\mathit{AB}}$ 上任意一点，过点 P作 PE⊥ OB于点 E，设 M为△ OPE的内心，当点 P从点 A运动到点 B时，则内心 M所经过的路径长为 　　．

如图，⊙ O为等腰三角形 ABC的外接圆， AB是⊙ O的直径， AB＝12， P为 $\stackrel{⏜}{\mathit{BC}}$ 上任意一点（不与点 B， C重合），直线 CP交 AB的延长线于点 Q，⊙ O在点 P处的切线 PD交 BQ于点 D，则下列结论：①若∠ PAB＝30°，则 $\stackrel{⏜}{\mathit{PB}}$ 的长为π；②若 PD∥ BC，则 AP平分∠ CAB；③若 PB＝ BD，则 PD＝6 $\sqrt{3}$ ；④无论点 P在 $\stackrel{⏜}{\mathit{BC}}$ 上的位置如何变化， CP• CQ＝108．其中正确结论的序号为 　　．

如图，正三角形 ABO的边长为2， O为坐标原点，点 A在 x轴上，点 B在第二象限，△ ABO沿 x轴正方向做无滑动的翻滚，经一次翻滚后得△ A ₁ B ₁ O，则翻滚三次后点 B的对应点的坐标是 　　，翻滚90次后 AB的中点 M经过的路径长为 　　．

如图，为的弦，直径为4，于，，则的长为　　（结果保留．

如图，为的弦，直径为4，于，，则的长为　　（结果保留．

如图，正方形内接于，为中点，连接，．

（1）求证：；

（2）当的半径为2时，求的长．

    如图所示的两段弧中，位于上方的弧半径为，下方的弧半径为，则　　．（填“”“ ”“ ”

如图，正方形OABC的边长为2，以O为圆心，EF为直径的半圆经过点A，连接AE，CF相交于点P，将正方形OABC从OA与OF重合的位置开始，绕着点O逆时针旋转90°，交点P运动的路径长是　　．

如图，△ABC中，∠C＝90°，∠A＝60°， $\mathit{AB}=2\sqrt{3}$．将△ABC沿直线CB向右作无滑动滚动一次，则点C经过的路径长是　　．