初中数学正多边形和圆填空题

据《汉书律历志》记载：“量者，龠yuè、合、升、斗、斛hú也”斛是中国古代的一种量器，“斛底，方而圜huán其外，旁有庣tiāo焉”．意思是说：“斛的底面为：正方形外接一个圆，此圆外是一个同心圆”，如图所示．

问题：现有一斛，其底面的外圆直径为两尺五寸（即2.5尺），“庣旁”为两寸五分（即两同心圆的外圆与内圆的半径之差为0.25尺），则此斛底面的正方形的周长为　　尺．（结果用最简根式表示）

如图，正六边形 $\mathit{ABCDEF}$内接于 $\odot O$，边长 $\mathit{AB}=2$，则扇形 $\mathit{AOB}$的面积为　　．

观察下列结论：

（1）如图①，在正三角形中，点，是，上的点，且，则，；

（2）如图2，在正方形中，点，是，上的点，且，则，；

（3）如图③，在正五边形中点，是，上的点，且，则，；

根据以上规律，在正边形中，对相邻的三边实施同样的操作过程，即点，是，上的点，且，与相交于．也会有类似的结论，你的结论是　　．

如图，边长为 $2\sqrt{3}\mathit{cm}$的正六边形螺帽，中心为点 $O$， $\mathit{OA}$垂直平分边 $\mathit{CD}$，垂足为 $B$， $\mathit{AB}=17\mathit{cm}$，用扳手拧动螺帽旋转 $90°$，则点 $A$在该过程中所经过的路径长为　　 $\mathit{cm}$．

刘徽是我国魏晋时期卓越的数学家，他在《九章算术》中提出了“割圆术”，利用圆的内接正多边形逐步逼近圆来近似计算圆的面积．如图，若用圆的内接正十二边形的面积来近似估计的面积，设的半径为1，则　　．

如图，正五边形 $\mathit{ABCDE}$和正三角形 $\mathit{AMN}$都是 $\odot O$的内接多边形，则 $\angle \mathit{BOM}=$　　．

如图，五边形是的内接正五边形，是的直径，则的度数是　　．

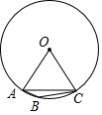
如图， $\mathit{AC}$是 $\odot O$的内接正六边形的一边，点 $B$在 $\stackrel{̂}{\mathit{AC}}$上，且 $\mathit{BC}$是 $\odot O$的内接正十边形的一边，若 $\mathit{AB}$是 $\odot O$的内接正 $n$边形的一边，则 $n=$　       　．

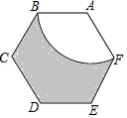
如图，正六边形 $\mathit{ABCDEF}$ 的边长为1，以点 $A$ 为圆心， $\mathit{AB}$ 的长为半径，作扇形 $\mathit{ABF}$ ，则图中阴影部分的面积为 　　（结果保留根号和 $\pi )$ ．

如图所示的正六边形 $\mathit{ABCDEF}$，连接 $\mathit{FD}$，则 $\angle \mathit{FDC}$的大小为　　．

如图，在拧开一个边长为 $a$ 的正六角形螺帽时，扳手张开的开口 $b=20\mathit{mm}$ ，则边长 $a=$ 　　 $\mathit{mm}$ ．

如图，正六边形ABCDEF内接于半径为3的圆O，则劣弧AB的长度为　　．

刘徽是中国古代卓越的数学家之一，他在《九章算术》中提出了“割圆术”，即用内接或外切正多边形逐步逼近圆来近似计算圆的面积，设圆 $O$的半径为1，若用圆 $O$的外切正六边形的面积 $S$来近似估计圆 $O$的面积，则 $S=$　　．（结果保留根号）

如图，正方形 $\mathit{ABCD}$内接于 $\odot O$，其边长为4，则 $\odot O$的内接正三角形 $\mathit{EFG}$的边长为　      　．

同一个圆的内接正方形和正三角形的边心距的比为 　　．