初中数学正多边形和圆试题

刘徽是我国魏晋时期卓越的数学家，他在《九章算术》中提出了“割圆术”，利用圆的内接正多边形逐步逼近圆来近似计算圆的面积．如图，若用圆的内接正十二边形的面积来近似估计的面积，设的半径为1，则　　．

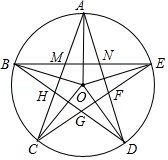
如图，、、、、是上的5等分点，连接、、、、，得到一个五角星图形和五边形．

（1）计算的度数；

（2）连接，证明：；

（3）求证：．

已知圆的半径是6，则圆内接正三角形的边长是　　．

如图，五边形是的内接正五边形，是的直径，则的度数是　　．

若正六边形的内切圆半径为2，则其外接圆半径为　　．

图中有两张型号完全一样的折叠式饭桌，将正方形桌面边上的四个弓形面板翻折起来后，就能形成一个圆形桌面（可近似看作正方形的外接圆），正方形桌面与翻折成的圆形桌面的面积之比最接近 $($ 　　 $)$

A．

$\frac{4}{5}$

B．

$\frac{3}{4}$

C．

$\frac{2}{3}$

D．

$\frac{1}{2}$

如图，已知 $\odot O$ 的内接正六边形 $\mathit{ABCDEF}$ 的边心距 $\mathit{OM}=2$ ，则该圆的内接正三角形 $\mathit{ACE}$ 的面积为 $($ 　　 $)$

A．

2

B．

4

C．

$6\sqrt{3}$

D．

$4\sqrt{3}$

如图，正五边形 $\mathit{ABCDE}$ 内接于 $\odot O$ ， $P$ 为 $\stackrel{̂}{\mathit{DE}}$ 上的一点（点 $P$ 不与点 $D$ 重合），则 $\angle \mathit{CPD}$ 的度数为 $($ 　　 $)$

A．

$30°$

B．

$36°$

C．

$60°$

D．

$72°$

如图，已知正五边形 $\mathit{ABCDE}$ 内接于 $\odot O$ ，连结 $\mathit{BD}$ ，则 $\angle \mathit{ABD}$ 的度数是 $($ 　　 $)$

A．

$60°$

B．

$70°$

C．

$72°$

D．

$144°$

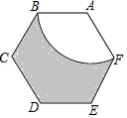
如图，正六边形 $\mathit{ABCDEF}$ 的边长为1，以点 $A$ 为圆心， $\mathit{AB}$ 的长为半径，作扇形 $\mathit{ABF}$ ，则图中阴影部分的面积为 　　（结果保留根号和 $\pi )$ ．

我们规定：一个正边形为整数，的最短对角线与最长对角线长度的比值叫做这个正边形的“特征值”，记为，那么　　．

若正六边形的边长为3，则其较长的一条对角线长为　　．

如图，正五边形的边长为1，对角线、相交于点，则四边形的周长为　．

如图，在正五边形中，与相交于点，则的度数为　　．

如图，在正六边形中，连接、，则的值为　　．