初中数学圆内接四边形的性质解答题

（1）如图1，将直角的顶点E放在正方形ABCD的对角线AC上，使角的一边交CD于点F，另一边交CB或其延长线于点G，求证：EF=EG；
（2）如图2，将（1）中的“正方形ABCD”改成“矩形ABCD”，其他条件不变．若AB=m，BC=n，试求的值；
（3）如图3，将直角顶点E放在矩形ABCD的对角线交点，EF、EG分别交CD与CB于点F、G，且EC平分∠FEG．若AB=2，BC=4，求EG、EF的长．

如图，在线段AE的同侧作正方形ABCD和正方形BEFG（BE＜AB），连接EG并延长交DC于点M，作MN⊥AB，垂足为N，MN交BD于点P，设正方形ABCD的边长为1．
（1）证明：四边形MPBG是平行四边形；
（2）设BE=x，四边形MNBG的面积为y，求y关于x的函数关系式，并写出自变量x的取值范围；
（3）如果按题设作出的四边形BGMP是菱形，求BE的长．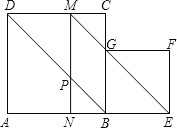

如图，在正方形ABCD中，点E、F分别是BC、CD的中点，DE交AF于点M，点N为DE的中点．
（1）若AB=4，求△DNF的周长及sin∠DAF的值；
（2）求证：2AD•NF=DE•DM．

如图，在边长为4的正方形ABCD中，动点E以每秒1个单位长度的速度从点A开始沿边AB向点B运动，动点F以每秒2个单位长度的速度从点B开始沿折线BC﹣CD向点D运动，动点E比动点F先出发1秒，其中一个动点到达终点时，另一个动点也随之停止运动，设点F的运动时间为t秒．

（1）点F在边BC上．
①如图1，连接DE，AF，若DE⊥AF，求t的值；
②如图2，连结EF，DF，当t为何值时，△EBF与△DCF相似？
（2）如图3，若点G是边AD的中点，BG，EF相交于点O，试探究：是否存在在某一时刻t，使得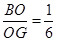？若存在，求出t的值；若不存在，请说明理由．

我们知道平行四边形有很多性质.
现在如果我们把平行四边形沿着它的一条对角线翻折，会发现这其中还有更多的结论.
【发现与证明】ABCD中，AB≠BC，将△ABC沿AC翻折至△AB′C，连结B′D.
结论1：B′D∥AC；
结论2：△AB′C与ABCD重叠部分的图形是等腰三角形.
……
请利用图1证明结论1或结论2（只需证明一个结论）.
【应用与探究】在ABCD中，已知∠B=30°，将△ABC沿AC翻折至△AB′C，连结B′D.
（1）如图1，若，则∠ACB=       °，BC=       ；
（2）如图2，，BC=1，AB′与边CD相交于点E，求△AEC的面积；
（3）已知，当BC长为多少时，是△AB′D直角三角形？

如图1，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF=BE．
（1）求证：CE=CF；
（2）在图1中，若G在AD上，且∠GCE=45°，则GE=BE+GD成立吗？为什么？
（3）根据你所学的知识，运用（1）、（2）解答中积累的经验，完成下列各题：
①如图2，在直角梯形ABCD中，AD∥BC（BC＞AD），∠B=90°，AB=BC=12，E是AB的中点，且∠DCE=45°，求DE的长；
②如图3，在△ABC中，∠BAC=45°，AD⊥BC，BD=2，CD=3，则△ABC的面积为　_________　（直接写出结果，不需要写出计算过程）．

在正方形ABCD中，AB=4．
（1）正方形ABCD的周长为         ；

（2）如图1，点E、F分别在BC和AD上，点P是线段EF上的动点，过点P作EF的垂线L，若直线L与正方形CD、AB的交点分别在G、H．
①求证：EF=GH；
②已知，BE=2，AF=1，若线段PE的长度为a，求a的最小值；
③如图2，在②的条件下，已知AH=，PE=2PF，求图中阴影部分的面积．

已知△ABC是等边三角形，D是BC边上的一个动点（点D不与B，C重合）△ADF是以AD为边的等边三角形，过点F作BC的平行线交射线AC于点E，连接BF．

（1）如图1，求证：△AFB≌△ADC；
（2）请判断图1中四边形BCEF的形状，并说明理由；
（3）若D点在BC 边的延长线上，如图2，其它条件不变，请问（2）中结论还成立吗？如果成立，请说明理由．

如图，二次函数的图象与x轴相交于点A（﹣3，0）、B（1，0），与y轴相交于点C，点G是二次函数图象的顶点，直线GC交x轴于点H（3，0），AD平行GC交y轴于点D．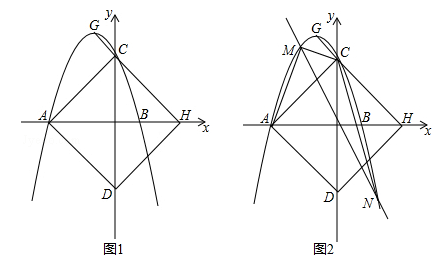

（1）求该二次函数的表达式；
（2）求证：四边形ACHD是正方形；
（3）如图2，点M（t，p）是该二次函数图象上的动点，并且点M在第二象限内，过点M的直线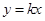交二次函数的图象于另一点N．
①若四边形ADCM的面积为S，请求出S关于t的函数表达式，并写出t的取值范围；
②若△CMN的面积等于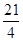，请求出此时①中S的值．

在矩形ABCD中，AB=a，AD=b，点M为BC边上一动点（点M与点B、C不重合），连接AM，过点M作MN⊥AM，垂足为M，MN交CD或CD的延长线于点N．

（1）求证：△CMN∽△BAM；
（2）设BM=x，CN=y，求y关于x的函数解析式．当x取何值时，y有最大值，并求出y的最大值；
（3）当点M在BC上运动时，求使得下列两个条件都成立的b的取值范围：①点N始终在线段CD上，②点M在某一位置时，点N恰好与点D重合．

如图，在△ABC中，AB=6，BC=9,AC=8，点P在△ABC内部，过点P分别画AB、BC、CA的平行线，与各边分别相交得线段DE、FG、HK，已知线段DE、FG、HK的长度都为d,求d的值．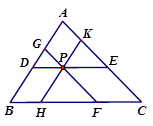

如图，菱形ABCD中，点P是CD的中点，∠BCD=60°，射线AP交BC的延长线于点E，射线BP交DE于点K，点O是线段BK的中点．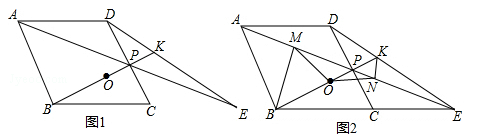

（1）求证：△ADP≌△ECP；
（2）若BP=n•PK，试求出n的值；
（3）作BM丄AE于点M，作KN丄AE于点N，连结MO、NO，如图2所示，请证明△MON是等腰三角形，并直接写出∠MON的度数．

如图1，直线 $l:y=-\frac{3}{4}x+b$与 $x$轴交于点 $A(4,0)$，与 $y$轴交于点 $B$，点 $C$是线段 $\mathit{OA}$上一动点 $(0<\mathit{AC}<\frac{16}{5})$．以点 $A$为圆心， $\mathit{AC}$长为半径作 $\odot A$交 $x$轴于另一点 $D$，交线段 $\mathit{AB}$于点 $E$，连接 $\mathit{OE}$并延长交 $\odot A$于点 $F$．

（1）求直线 $l$的函数表达式和 $\tan \angle \mathit{BAO}$的值；

（2）如图2，连接 $\mathit{CE}$，当 $\mathit{CE}=\mathit{EF}$时，

①求证： $\mathit{\Delta OCE}\backsim \mathit{\Delta OEA}$；

②求点 $E$的坐标；

（3）当点 $C$在线段 $\mathit{OA}$上运动时，求 $\mathit{OE}\cdot \mathit{EF}$的最大值．

如图，将▱ABCD的AD边延长至点E，使DE=AD，连接CE，F是BC边的中点，连接FD．

（1）求证：四边形CEDF是平行四边形；
（2）若AB=3，AD=4，∠A=60°，求CE的长．

在边长为1的小正方形组成的方格纸中，若多边形的各顶点都在方格纸的格点（横竖格子线的交错点）上，这样的多边形称为格点多边形．记格点多边形内的格点数为a，边界上的格点数为b，则格点多边形的面积可表示为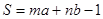，其中m，n为常数．

（1）在下面的方格中各画出一个面积为6的格点多边形，依次为三角形、平行四边形（非菱形）、菱形；
（2）利用（1）中的格点多边形确定m，n的值．