初中数学圆内接四边形的性质解答题

如图，点E，F分别是锐角∠A两边上的点，AE=AF，分别以点E，F为圆心，以AE的长为半径画弧，两弧相交于点D，连接DE，DF．

（1）请你判断所画四边形的形状，并说明理由；
（2）连接EF，若AE=8厘米，∠A=60°，求线段EF的长．

如图，在正方形ABCD中，点E、F分别在BC和CD上，AE=AF．

（1）求证：BE=DF
（2）连接AC交EF于点D，延长OC至点M，使OM=OA，连结EM、FM，试证明四边形AEMF是菱形．

如图，一次函数y₁=mx+n的图象与x轴、y轴分别交于A、B两点，与反比例函数y₂=（x＜0）交于点C，过点C分别作x轴、y轴的垂线，垂足分别为点E、F．若OB=2，CF=6，．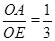

（1）求点A的坐标；
（2）求一次函数和反比例函数的表达式．

如图，在四边形ABCD中，AB⊥BC，CD⊥BC，AB=2，BC=CD=4，AC、BD交于点O，在线段BC上，动点M以每秒1个单位长度的速度从点C出发向点B做匀速运动，同时动点N从点B出发向点C做匀速运动，当点M、N其中一点停止运动时，另一点也停止运动，分别过点M、N做BC的垂线，分别交AC、BD于点E、F，连接EF．若运动时间为x秒，在运动过程中四边形EMNF总为矩形（点M、N重合除外）．

（1）求点N的运动速度；
（2）当x为多少时，矩形EMNF为正方形？
（3）当x为多少时，矩形EMNF的面积S最大？并求出最大值．

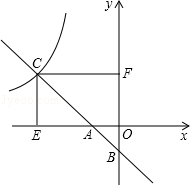
如图，在四边形ABCD中，AD∥BC，AE=2EB，AD=2，BC=5，EF∥DC，交BC于点F，连接AF．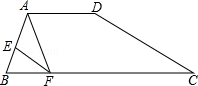

（1）求CF的长；
（2）若∠BFE=∠FAB，求AB的长．

如图，在▱ABDC中，分别取AC、BD的中点E和F，连接BE、CF，过点A作AP∥BC，交DC的延长线于点P．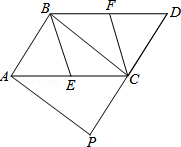

（1）求证：△ABE≌△DCF；
（2）当∠P满足什么条件时，四边形BECF是菱形？证明你的结论．

如图，∠BAP+∠APD=180°，∠1=∠2，求证：∠E=∠F．

已知：如图，在四边形ABCD中，AB∥CD，∠B=∠D，P为对角线AC上的一点，PE⊥AB于E，PF⊥AD于F，且PE=PF．求证：四边形ABCD是菱形．

已知：矩形ABCD中，对角线AC与BD交于点O，∠BOC=120°，AC=4cm，求矩形ABCD的周长．

已知平行四边形ABCD中，AE平分∠BAD，CF平分∠BCD，分别交CD、AB于E、F，求证：AE=CF．

如图1，矩形纸片ABCD的边长AB=4cm，AD=2cm．同学小明现将该矩形纸片沿EF折痕，使点A与点C重合，折痕后在其一面着色（如图2），观察图形对比前后变化，回答下列问题：

（1）GF      FD：（直接填写=、＞、＜）
（2）判断△CEF的形状，并说明理由；
（3）小明通过此操作有以下两个结论：
①四边形EBCF的面积为4cm²
②整个着色部分的面积为5．5cm²
运用所学知识，请论证小明的结论是否正确．

如图，在平行四边形ABCD中，点E、F分别在BC、AD上，且∠BAE=∠DCF．

（1）求证：△ABE≌△CDF；
（2）若AC⊥EF，试判断四边形AECF是什么特殊四边形，并证明你的结论．

如图，在菱形ABCD中，AB=2，∠DAB=60°，点E是AD边的中点．点M是AB边上一动点（不与点A重合），延长ME交射线CD于点N，连接MD、AN．

（1）求证：四边形AMDN是平行四边形；
（2）填空：
①当AM的值为              时，四边形AMDN是矩形；
②当AM的值为                  时，四边形AMDN是菱形．

已知：如图，在平行四边形ABCD中，点E、F在AC上，且AE=CF．
求证：四边形BEDF是平行四边形．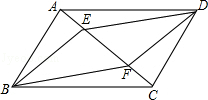

如图1，四边形ABCD为矩形，E为边BC上一点，G为边AD上一点，四边形AEGF为菱形．

（1）如图2，当G与D重合时，求证：E为BC的中点；
（2）若AB=3，菱形AEGF为正方形，且EC＜EG，求AD的取值范围．