河北省廊坊市三河市八年级下学期期末数学试卷
顺次连接四边形各边中点所得的四边形是( )
| A.平行四边形 | B.矩形 | C.菱形 | D.以上都不对 |
已知三组数据:①2,3,4;②3,4,5;③1, ,2.分别以每组数据中的三个数为三角形的三边长,构成直角三角形的有( )
,2.分别以每组数据中的三个数为三角形的三边长,构成直角三角形的有( )
| A.② | B.①② | C.①③ | D.②③ |
为了调查某小区居民的用水情况,随机抽查了若干户家庭的月用水量,结果如下表:
| 月用水量(吨) |
3 |
4 |
5 |
8 |
| 户 数 |
2 |
3 |
4 |
1 |
则关于这若干户家庭的月用水量,下列说法错误的是( )
A.众数是4 B.平均数是4.6 C.调查了10户家庭的月用水量 D.中位数是4.5
下列命题中,真命题是( )
| A.对角线相等的四边形是矩形 |
| B.对角线互相垂直的四边形是菱形 |
| C.对角线互相平分的四边形是平行四边形 |
| D.对角线互相垂直平分的四边形是正方形 |
矩形ABCD中,对角线AC,BD相交于点O,∠AOB=60°,AB=6cm,则BD的长( )
| A.6cm | B.8cm | C.10cm | D.12cm |
小王从A地前往B地,到达后立刻返回.他与A地的距离y(千米)和所用时间x(小时)之间的函数关系如图所示,则小王出发6小时后距A地( )千米.
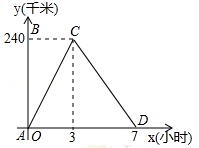
| A.40 | B.60 | C.80 | D.120 |
期末考试后,办公室里有两位数学老师正在讨论他们班的数学考试成绩,林老师:“我班的学生考得还不错,有一半的学生考79分以上,一半的学生考不到79分.”王老师:“我班大部分的学生都考在80分到85分之间喔.”依照上面两位老师所叙述的话你认为林、王老师所说的话分别针对( )
| A.平均数、众数 | B.平均数、极差 | C.中位数、方差 | D.中位数、众数 |
如图,在平面直角坐标系中,点A(2,m)在第一象限,若点A关于x轴的对称点B在直线y=﹣x+1上,则m的值为( )
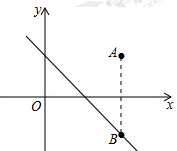
| A.﹣1 | B.1 | C.2 | D.3 |
如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF,②∠DAF=15°,③AC垂直平分EF,④BE+DF=EF,⑤S△CEF=2S△ABE.其中正确结论有( )个.

A.2 B.3 C.4 D.5
一次函数y=﹣2x+b中,当x=1时,y<1,当x=﹣1时,y>0.则b的取值范围是 .
学校以德智体三项成绩来计算学生的平均成绩,三项成绩的比例依次为1:3:1,小明德智体三项成绩分别为96分,95分,94分,则小明的平均成绩为 分.
如图是由边长为1m的正方形地砖铺设的地面示意图,小明沿图中所示的折线从A⇒B⇒C所走的路程为 m.

如图,直线y=2x+4与x,y轴分别交于A,B两点,以OB为边在y轴右侧作等边三角形OBC,将点C向左平移,使其对应点C′恰好落在直线AB上,则点C′的坐标为 .

如图1,平行四边形纸片ABCD的面积为120,AD=20,AB=18.今沿两对角线将四边形ABCD剪成甲、乙、丙、丁四个三角形纸片.若将甲、丙合并(AD、CB重合)形成对称图形戊,如图2所示,则图形戊的两条对角线长度之和是 .

如图,Rt△ABC中,∠C=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC=5,OC=6 ,则另一直角边BC的长为 .
,则另一直角边BC的长为 .

如图,点E,F分别是锐角∠A两边上的点,AE=AF,分别以点E,F为圆心,以AE的长为半径画弧,两弧相交于点D,连接DE,DF.
(1)请你判断所画四边形的形状,并说明理由;
(2)连接EF,若AE=8厘米,∠A=60°,求线段EF的长.
在三河市创建文明城区的活动中,有两段长度相等的彩色道砖铺设任务,分别交给甲、乙两个施工队同时进行施工.如图是反映所铺设彩色道砖的长度y(米)与施工时间x(时)之间关系的部分图象.请解答下列问题:
(1)求乙队在0≤x≤2的时段内的施工速度;
(2)求乙队在2≤x≤6的时段内,y与x之间的函数关系式;
(3)如果甲队施工速度不变,乙队在开挖6小时后,施工速度增加到12米/时,结果两队同时完成了任务.求甲队从开始施工到完工所铺设的彩色道砖的长度为多少米?
我市某中学举行“中国梦•校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.
(1)根据图示填写下表;
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.
| |
平均数 |
中位数 |
众数 |
| 初中部 |
|
85 |
|
| 高中部 |
85 |
|
100 |

如图,直线l1的解析表达式为y=3x﹣3,且l1与x轴交于点D,直线l2经过点A,B,直线l1,l2交于点C.
(1)求点D的坐标;
(2)求△ADC的面积;
(3)在直线l2上存在异于点C的另一点P,使得△ADP与△ADC的面积相等,请直接写出点P的坐标;
(4)在坐标平面内是否存在这样的点H,使以A,D,C,H为顶点的四边形是平行四边形?若存在,请直接写出满足条件的点H的个数.
如图1,在△OAB中,∠OAB=90°,∠AOB=30°,OB=8.以OB为边,在△OAB外作等边△OBC,D是OB的中点,连接AD并延长交OC于E.
(1)求证:四边形ABCE是平行四边形;
(2)如图2,将图1中的四边形ABCO折叠,使点C与点A重合,折痕为FG,求OG的长.
某学校为鼓励学生加强体育锻炼,2014-2015学年八年级(一)班准备购买10副某种品牌的羽毛球拍,每副球拍配x(x≥2)个羽毛球,该学校附近A、B两家超市都有这种品牌的羽毛球拍和羽毛球出售,且每副球拍的标价均为30元,每个羽毛球的标价为3元,目前两家超市同时在做促销活动:
A超市:所有商品均打九折(按标价的90%)销售;
B超市:买一副羽毛球拍送两个羽毛球.
设在A超市购买羽毛球拍和羽毛球的费用为yA(元),在B超市购买羽毛球拍和羽毛球的费用为yB(元).请解答下列问题:
(1)分别写出yA、yB与x之间的关系式;
(2)函数yA、yB的图象是否存在交点?若存在,求出交点坐标,并说明该点的实际意义;若不存在,请说明理由.
(3)若该活动中心只在一家超市购买,你认为在哪家超市购买更划算?
(4)若每副球拍配15个羽毛球,请你帮助该活动中心设计出最省钱的购买方案.




 有意义,则x的取值范围为 .
有意义,则x的取值范围为 . ﹣(﹣2015)0+(
﹣(﹣2015)0+( )﹣1+|
)﹣1+| ﹣1|.
﹣1|.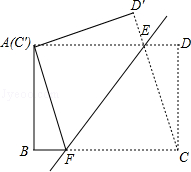
 粤公网安备 44130202000953号
粤公网安备 44130202000953号