如图，点E，F分别是锐角∠A两边上的点，AE=AF，分别以点E，F为圆心，以AE的长为半径画弧，两弧相交于点D，连接DE，DF．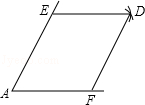
（1）请你判断所画四边形的形状，并说明理由；
（2）连接EF，若AE=8厘米，∠A=60°，求线段EF的长．
相关知识点
推荐套卷
如图，点E，F分别是锐角∠A两边上的点，AE=AF，分别以点E，F为圆心，以AE的长为半径画弧，两弧相交于点D，连接DE，DF．
（1）请你判断所画四边形的形状，并说明理由；
（2）连接EF，若AE=8厘米，∠A=60°，求线段EF的长．
粤公网安备 44130202000953号