(1)如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE.
①∠AEB的度数为 ;
②线段AD,BE之间的数量关系为 ;
(2)如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE中DE边上的高,连接BE,请判断∠AEB的度数及线段CM,AE,BE之间的数量关系,并说明理由;
(3)如图3,在正方形ABCD中,CD= ,若点P满足PD=1,且∠BPD=90°,请求出点A到BP的距离.
,若点P满足PD=1,且∠BPD=90°,请求出点A到BP的距离.
如图,点P是菱形ABCD的对角线BD上一点,连结AP、CP,延长CP交AD于E,交BA的延长线于F.
(1)求证:∠DCP=∠DAP;
(2)若AB=2,DP:PB=1:2,且PA⊥BF,求对角线BD的长.
已知:如图,▱ABCD中,E、F分别是边AB、CD的中点.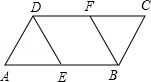
(1)求证:四边形EBFD是平行四边形;
(2)若AD=AE=2,∠A=60°,求四边形EBFD的周长.
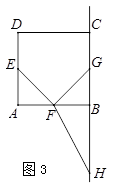
在正方形ABCD中,点E,F,G分别是边AD,AB,BC的中点,点H是直线BC上一点.将线段FH绕点F逆时针旋转90º,得到线段FK,连接EK.
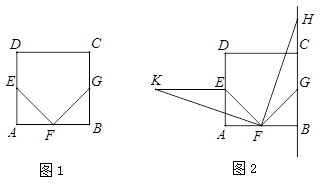
(1)如图1,求证:EF=FG,且EF⊥FG;
(2)如图2,若点H在线段BC的延长线上,猜想线段BH,EF,EK之间满足的数量关系,并证明你的结论.
(3)若点H在线段BC的反向延长线上,请在图3中补全图形并直接写出线段BH,EF,EK之间满足的数量关系.
如图,矩形ABCD中,∠ACB=30°,将一块直角三角板的直角顶点P放在两对角线AC,BD的交点处,以点P为旋转中心转动三角板,并保证三角板的两直角边分别于边AB,BC所在的直线相交,交点分别为E,F.
(1)当PE⊥AB,PF⊥BC时,如图1,则 的值为 ;
的值为 ;
(2)现将三角板绕点P逆时针旋转α(0°<α<60°)角,如图2,求 的值;
的值;
(3)在(2)的基础上继续旋转,当60°<α<90°,且使AP:PC=1:2时,如图3, 的值是否变化?证明你的结论.
的值是否变化?证明你的结论.
如图,正方形ABCD的边长为4,E是BC边的中点,点P在射线AD上,过P作PF⊥AE于F.
(1)求证:△PFA∽△ABE;
(2)若AP= ,求△PFA的面积.
,求△PFA的面积.
如图,点E、F、G、H分别为矩形ABCD四条边的中点,证明:四边形EFGH是菱形.
已知:如图,点E,F是□ABCD中AB,DC边上的点,且AE=CF,联结DE,BF.
求证:DE =BF.
已知:如图,E,F是▱ABCD的对角线AC上两点,且AE=CF.求证:BE=DF.
如图,在正方形ABCD中,点E、F在对角线BD上,且BF=DE.
⑴求证:四边形AECF是菱形.
⑵若AB=2,BF=1,求四边形AECF的面积.
已知:如图,平行四边形ABCD中,∠BCD的平分线交AB于E,交DA的延长线于F.
求证:AE=AF.