某个长方体主视图是边长为1cm的正方形.沿这个正方形的对角线向垂直于正方形的方向将长方体切开,截面是一个正方形.那么这个长方体的俯视图是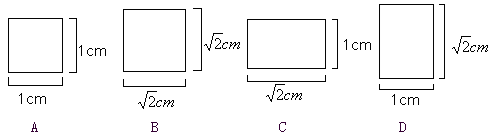
图①是一个边长为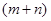 的正方形,小颖将图①中的阴影部分拼成图②的形状,由图①和图②能验证的式子是( )
的正方形,小颖将图①中的阴影部分拼成图②的形状,由图①和图②能验证的式子是( )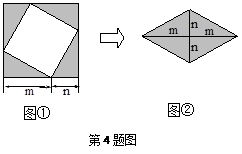
A.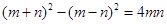 |
B.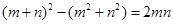 |
C.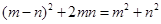 |
D.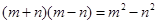 |
如图,在梯形ABCD中,AB∥CD,AD=BC,对角线AC⊥BD,垂足为O.
若CD=3,AB=5,则AC的长为
A. |
B.4 | C. |
D.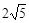 |
如图,每个小正方形的边长为1,A、B、C是小正方形的顶点,则∠ABC的度数为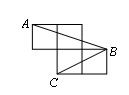
| A.90° | B.60° | C.45° | D.30° |
如图,等腰梯形ABCD内接于半圆D,且AB = 1,BC = 2,则OA =( ).
A. |
B. |
C. |
D. |
如图,梯形ABCD的对角线AC、BD相交于O,G是BD的中点.
若AD = 3,BC = 9,则GO: BG =( ).
| A.1 : 2 | B.1 : 3 | C.2 : 3 | D.11 : 20 |
如图,梯形 中,
中, 点
点 在
在 上,
上, 点
点 是
是 的中点,且
的中点,且 若
若 则
则 的长为
的长为
A. |
B. |
C. |
D. |
如图,矩形ABCD中,AB>AD,AB=a,AN平分∠DAB,DM⊥AN于点M,CN⊥AN于点N.则DM+CN的值为(用含a的代数式表示)(▲)
| A.a | B. |
C. |
D. |
梯形ABCD中,AD∥BC,AB=CD=AD=2,∠B=60°,则下底BC的长是(▲)
| A.3 | B.4 | C.2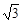 |
D.2+2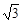 |
如图在平面直角坐标系中,□ MNEF的两条对角线ME,NF交于原点O,
点F的坐标是(3,2),则点N的坐标为( )。
| A.(-3,-2) | B.(-3,2) | C.(-2,3) | D.(2,3) |
如图(十九),用四个螺丝将四条不可弯曲的木条围成一个木框,不计螺丝大小,其中相邻两螺丝的距离依序为2、3、4、6,且相邻两木条的夹角均可调整。若调整木条的夹角时不破坏此木框,则任两螺丝的距离之最大值为何?
| A.5 | B.6 | C.7 | D.10 |
如图(十五)梯形ABCD的两底长为 =6,
=6,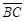 =10,中线为
=10,中线为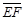 ,且ÐB=90°,若P为
,且ÐB=90°,若P为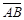 上的一点,且
上的一点,且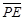 将梯形ABCD分成面积相 同的两区域,则△EFP与梯形ABCD的面积比为何?
将梯形ABCD分成面积相 同的两区域,则△EFP与梯形ABCD的面积比为何?
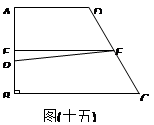
| A.1:6 | B.1:10 | C.1:12 | D.1:16 |
图(十)为一个平行四边形ABCD,其中H、G两点分别在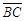 、
、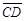 上,
上, ^
^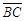 ,
, ^
^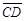 ,且
,且 、
、 、
、 将ÐBAD分成 Ð1、Ð2、Ð3、Ð4四个角。若
将ÐBAD分成 Ð1、Ð2、Ð3、Ð4四个角。若 =5,
=5, =6,则下列关系何者正确?
=6,则下列关系何者正确?

| A.Ð1=Ð2 | B.Ð3=Ð4 | C.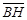 = = |
D.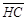 = =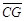 |
如图所示,矩形ABCD中,AB=4,BC= ,点E是折线段A-D-C上的一个动点(点E与点A不重合),点P是点A关于BE的对称点.
,点E是折线段A-D-C上的一个动点(点E与点A不重合),点P是点A关于BE的对称点.
在点E运动的过程中,使△PCB为等腰三角形的点E的位置共有
| A.2个 | B.3个 | C.4个 | D.5个 |