初中数学圆内接四边形的性质选择题

正方形ABCD、正方形BEFG和正方形DMNK的位置如图所示，点A在线段NF上，AE=8，则△NFP的面积为（ ）．

A．30      B．32        C．34     D．36

如图，3个全等的菱形按如图方式拼合在一起，恰好得到一个边长相等的六边形，则菱形较长的对角线与较短的对角线之比是（ ）．

A．

B．

C．

D．

如图，矩形ABCD中，AB=1，AD=2，M是CD的中点，点P在矩形的边上沿A→B→C→M运动，则△APM的面积y与点P经过的路程x之间的函数关系用图象表示大致是（ ）

如图，在矩形ABCD中，AC、BD相交于点O，AE平分∠BAD交BC于E，若∠EAO=15°，则∠BOE的度数为（ ）．

A．85°        B．80°        C．75°        D．70°

如图，菱形ABCD的对角线AC、BD的长分别是6cm、8cm，AE⊥BC于点E，则AE的长是（ ）．

A．cm        B．cm        C．cm        D．cm

如果一个多边形的每一个外角都是45°，那么这个多边形的内角和是（   ）

A．540°

B．720°

C．1080°

D．1260°

如图，四边形ABCD中，AC=a，BD=b，且AC⊥BD，顺次连接四边形ABCD各边中点，得到四边形A₁B₁C₁D₁，再顺次连接四边形A₁B₁C₁D₁各边中点，得到四边形A₂B₂C₂D₂，如此进行下去，得到四边形A_nB_nC_nD_n．下列结论正确的是（ ）
①四边形A₄B₄C₄D₄是菱形；
②四边形A₃B₃C₃D₃是矩形；
③四边形A₇B₇C₇D₇周长为；
④四边形A_nB_nC_nD_n面积为．

A．①②③

B．②③④

C．①③④

D．①②③④

在矩形ABCD中，AD=3AB，点G、H分别在AD、BC上，连BG、DH，且BG∥DH，当=（ ）时，四边形BHDG为菱形．

A. B. C. D.

正方形具有而菱形不一定具有的性质是（ ）

A．对角线相等	B．对角线互相垂直平分
C．对角线平分一组对角	D．四条边相等

下列四个命题，其中真命题是（   ）

A．方程的解是

B．3的平方根是

C．有两边和一个角分别对应相等的两个三角形全等

D．连接任意四边形各边中点的四边形是平行四边形

如图，将一个长为10cm，宽为8cm的矩形纸片对折两次后，沿所得矩形两邻边中点的连线（虚线）剪下，再打开，得到的菱形的面积为（ ）

A．10cm^2

B．20cm^2

C．40cm^2

D．80cm^2

下列命题是假命题的是（ ）

A．不在同一直线上的三点确定一个圆

B．正六边形的内角和是720°

C．矩形的对角线互相垂直且平分

D．角平分线上的点到角两边的距离相等

小明在学习了正方形之后，给同桌小文出了道题，从下列四个条件：①AB=BC，②∠ABC=90°，③AC=BD，④AC⊥BD中选两个作为补充条件，使▱ABCD为正方形（如图），现有下列四种选法，你认为其中错误的是（ ）

A．①②

B．②③

C．①③

D．②④

如图，图1、图2、图3分别表示甲、乙、丙三人由A地到B地的路线图（箭头表示行进的方向）．其中E为AB的中点，AH＞HB，判断三人行进路线长度的大小关系为（ ）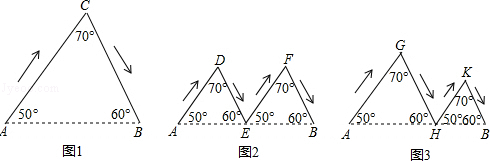

A．甲＜乙＜丙	B．乙＜丙＜甲
C．丙＜乙＜甲	D．甲=乙=丙

下列命题中，不正确的是（ ）

A．对角线相等的平行四边形是矩形

B．对角线互相垂直的四边形是菱形

C．三角形的中位线平行于第三边且等于第三边的一半

D．三角形的一条中线能将三角形分成面积相等的两部分