初中数学圆内接四边形的性质选择题

下列说法正确的是（    ）

A．一组对边相等，另一组对边平行的四边形是平行四边形

B．对角线互相垂直的四边形是菱形

C．对角线相等的四边形是矩形

D．对角线互相垂直平分且相等的四边形是正方形

如图，3个全等的菱形按如图方式拼合在一起，恰好得到一个边长相等的六边形，则菱形较长的对角线与较短的对角线之比是（ ）．

A．

B．

C．2

D．

如图，点A、B分别在射线OM、ON上，C、D分别是线段OA和OB上的点，以OC、OD为邻边作平行四边形OCED，下面给出三种作法的条件：①取OC=OA、OD=OB； ②取OC=OA、OD=OB；③取OC=OA、OD=OB．能使点E落在阴影区域内的作法有（ ）

A．①     B．①②     C．①②③     D．②③

用直尺和圆规作一个菱形，如图，能得到四边形ABCD是菱形的依据是（ ）

A．一组邻边相等的四边形是菱形

B．四边相等的四边形是菱形

C．对角线互相垂直的平行四边形是菱形

D．每条对角线平分一组对角的平行四边形是菱形

如图，AD是正五边形ABCDE的一条对角线，则∠BAD等于（ ）．

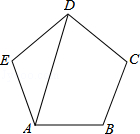
A．72°

B．108°

C．36°

D．62°

如图，点A、B分别在射线OM、ON上，C、D分别是线段OA和OB上的点，以OC、OD为邻边作平行四边形OCED，下面给出三种作法的条件：①取OC=OA、OD=OB； ②取OC=OA、OD=OB；③取OC=OA、OD=OB．能使点E落在阴影区域内的作法有（ ）

A．①     B．①②     C．①②③     D．②③

用直尺和圆规作一个菱形，如图，能得到四边形ABCD是菱形的依据是（ ）

A．一组邻边相等的四边形是菱形

B．四边相等的四边形是菱形

C．对角线互相垂直的平行四边形是菱形

D．每条对角线平分一组对角的平行四边形是菱形

如图，在▱ABCD中，DB=DC，∠C=65°，AE⊥BD于点E，则∠DAE等于（ ）

A．20°

B．25°

C．30°

D．35°

如图，点O是矩形ABCD的中心，E是AB上的点，折叠后，点B恰好与点O重合，若BC=3，则折痕CE的长为（   ）

A．

B．

C．3

D．6

顺次连接四边形ABCD四边中点得到新的四边形为菱形，那么原四边形ABCD为（  ）

A．矩形

B．菱形

C．对角线相等的四边形

D．对角线垂直的四边形

已知菱形的对角线分别长为6和8，则该菱形的周长为（  ）

A．5

B．15

C．20

D．24

如图，在菱形ABCD中，AB=5，对角线AC=6．若过点A作AE⊥BC，垂足为E，则AE的长为（ ）．

A．4

B．

C．

D．5

如图，在四边形ABCD中，E、F、G、H分别是AB、BD、CD、AC的中点，要使四边形EFGH是菱形，则四边形ABCD只需要满足一个条件，是（   ）

A．四边形ABCD是梯形     B．四边形ABCD是菱形
C．对角线AC="BD"          D．AD=BC

在菱形ABCD中，对角线AC长为3cm，∠ABC=60°，则菱形ABCD的周长为（ ）．

A．6cm

B．12cm

C．12cm

D．24cm

矩形具有而菱形不具有的性质是（ ）

A．两组对边分别平行	B．对角线相等
C．对角线互相平分	D．两组对角分别相等