山东省济南市平阴县中考二模数学试卷
如图所示,已知AB∥CD,EF平分∠CEG,∠1=80°,则∠2的度数为( )
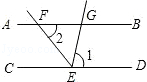
| A.20° | B.40° | C.50° | D.60° |
环境空气质量问题已经成为人们日常生活所关心的重要问题,我国新修订的《环境空气质量标准》中增加了PM2.5检测指标,“PM2.5”是指大气中危害健康的直径小于或等于2.5微米的颗粒物,2.5微米即0.0000025米.用科学记数法表示0.0000025为( )
| A.2.5×10﹣5 | B.2.5×105 | C.2.5×10﹣6 | D.2.5×106 |
为了大力宣传节约用电,某小区随机抽查了10户家庭的月用电量情况,统计如下表.关于这10户家庭的月用电量说法正确的是( )
| 月用电量(度) |
25 |
30 |
40 |
50 |
60 |
| 户数 |
1 |
4 |
2 |
2 |
1 |
A.平均数是38.5 B.众数是4 C.中位数是40 D.极差是3
如图,在▱ABCD中,E是AD边上的中点,连接BE,并延长BE交CD延长线于点F,则△EDF与△BCF的周长之比是( )

| A.1:2 | B.1:3 | C.1:4 | D.1:5 |
下列函数中,在0≤x≤2上y随x的增大而增大的是( )
| A.y="-x+1" | B.y=x2-4x+5 | C.y=x2 | D.y= |
下列命题中,不正确的是( )
| A.对角线相等的平行四边形是矩形 |
| B.对角线互相垂直的四边形是菱形 |
| C.三角形的中位线平行于第三边且等于第三边的一半 |
| D.三角形的一条中线能将三角形分成面积相等的两部分 |
已知函数y=-(x-m)(x-n)(其中m<n)的图象如图所示,则一次函数y=mx+n与反比例函数y= 的图象可能是( )
的图象可能是( )

如图,菱形OABC的顶点O在坐标系原点,顶点A在x轴上,∠B=120°,OA=2,将菱形OABC绕原点O顺时针旋转105°至OA′B′C′的位置,则点B′的坐标为( )
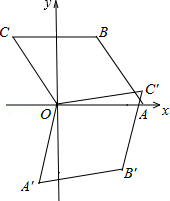
A.(-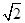 , ,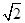 ) ) |
B.(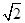 ,- ,-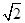 ) ) |
C.(2,-2) | D.(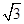 ,- ,-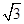 ) ) |
在平面直角坐标系xOy中,对于点P(x,y),我们把点P(-y+1,x+1)叫做点P的伴随点.已知点A1的伴随点为A2,点A2的伴随点为A3,点A3的伴随点为A4,…,这样依次得到点A1,A2,A3,…,An,….例如:点A1的坐标为(3,1),则点A2的坐标为(0,4),…;若点A1的坐标为(a,b),则点A2015的坐标为( )
| A.(-b+1,a+1) | B.(-a,-b+2) |
| C.(b-1,-a+1) | D.(a,b) |
如图,AB是⊙O的直径,C、D是⊙O上的点,∠CDB=20°,过点C作⊙O的切线交AB的延长线于点E,则∠E= .

新定义:[a,b,c]为函数y=ax2+bx+c (a,b,c为实数)的“关联数”.若“关联数”为[m-2,m,1]的函数为一次函数,则m的值为 .
如图,Rt△ABO中,∠AOB=90°,点A在第一象限、点B在第四象限,且AO:BO=1: ,若点A(x0,y0)的坐标x0,y0满足y0=
,若点A(x0,y0)的坐标x0,y0满足y0= ,则点B(x,y)的坐标x,y所满足的关系式为 .
,则点B(x,y)的坐标x,y所满足的关系式为 .

(1)如图,正方形AEFG的顶点E、G在正方形ABCD的边AB、AD上,连接BF、DF.求证:BF=DF;
(2)如图,在▱ABCD中,AD=4,AB=8,∠A=30°,以点A为圆心,AD的长为半径画弧交AB于点E,连接CE,求阴影部分的面积.(结果保留π)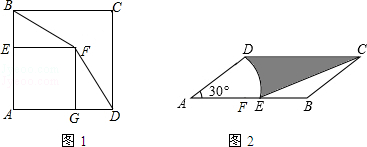
某商店需要购进甲、乙两种商品共160件,其进价和售价如下表:(注:利润=售价-进价)
| |
甲 |
乙 |
| 进价(元/件) |
15 |
35 |
| 售价(元/件) |
20 |
45 |
若商店计划销售完这批商品后能使利润达到1100元,问甲、乙两种商品应分别购进多少件?
我县某中学艺术节期间,向全校学生征集书画作品.九年级美术王老师从全年级14个班中随机抽取了A、B、C、D四个班,对征集到的作品的数量进行了分析统计,制作了如下两幅不完整的统计图.
(1)王老师所调查的4个班共征集到作品多少件?请把图2补充完整;
(2)如果全年级参展作品中有5件获得一等奖,其中有3名作者是男生,2名作者是女生.现在要在其中抽两人去参加学校总结表彰座谈会,求恰好抽中一男一女的概率.(要求写出用树状图或列表分析过程)
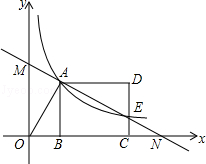
如图,反比例函数y= (x>0)的图象经过线段OA的端点A,O为原点,作AB⊥x轴于点B,点B的坐标为(2,0),tan∠AOB=
(x>0)的图象经过线段OA的端点A,O为原点,作AB⊥x轴于点B,点B的坐标为(2,0),tan∠AOB=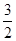 .
.
(1)求k的值;
(2)将线段AB沿x轴正方向平移到线段DC的位置,反比例函数y= (x>0)的图象恰好经过DC上一点E,且DE:EC=2:1,求直线AE的函数表达式;
(x>0)的图象恰好经过DC上一点E,且DE:EC=2:1,求直线AE的函数表达式;
(3)若直线AE与x轴交于点,N,与y轴交于点M,请你探索线段AM与线段NE的大小关系,写出你的结论并说明理由.
已知:如图①,在Rt△ACB中,∠C=90°,AC=4cm,BC=3cm,点P由B出发沿BA方向向点A匀速运动,速度为1cm/s;点Q由A出发沿AC方向向点C匀速运动,速度为2cm/s;连接PQ.若设运动的时间为t(s)(0<t<2),解答下列问题:
(1)当t为何值时,PQ∥BC;
(2)设△AQP的面积为y(cm2),求y与t之间的函数关系式;
(3)是否存在某一时刻t,使线段PQ恰好把Rt△ACB的周长和面积同时平分?若存在,求出此时t的值;若不存在,说明理由;
(4)如图②,连接PC,并把△PQC沿QC翻折,得到四边形PQP′C,那么是否存在某一时刻t,使四边形PQP′C为菱形?若存在,求出此时菱形的边长;若不存在,说明理由.

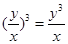



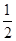





 的解是( )
的解是( )
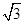 )0= .
)0= . 的解是 .
的解是 .

 ;并求它的最小整数解.
;并求它的最小整数解.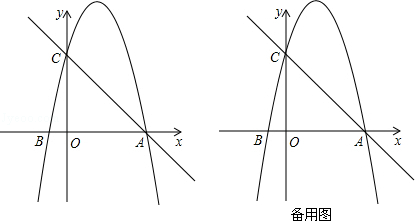
 粤公网安备 44130202000953号
粤公网安备 44130202000953号