初中数学圆内接四边形的性质试题

如图，纸上有五个边长为1的小正方形组成的图形纸，我们可以把它剪开拼成一个正方形．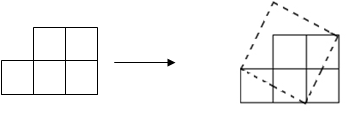

（1）拼成的正方形的面积与边长分别是多少？
（2）如图所示，以数轴的单位长度的线段为边作一个直角三角形，以数轴的-1点为圆心，直角三角形的最大边为半径画弧，交数轴正半轴于点A，那么点A表示的数是多少？点A表示的数的相反数是多少？
（3）你能把十个小正方形组成的图形纸，剪开并拼成正方形吗？若能，请画出示意图，并求它的边长

（1）如图1，已知△ABC，以AB、AC为边向△ABC外作等边△ABD和等边△ACE，连接BE，CD，请你完成图形（尺规作图，保留作图痕迹），并猜想BE与CD的关系：___________；你是通过证明_______________ 得到的。
（2）如图2，已知△ABC，以AB、AC为边向外作正方形ABFD和正方形ACGE，连接BE，CD，BE与CD有什么数量关系？并说明理由；
（3）运用（1）、（2）解答中所积累的经验和知识，完成下题：
如图3，要测量池塘两岸相对的两点B，E的距离，已经测得∠ABC=45°，∠CAE=90°，AB=BC=100米，AC=AE，求BE的长．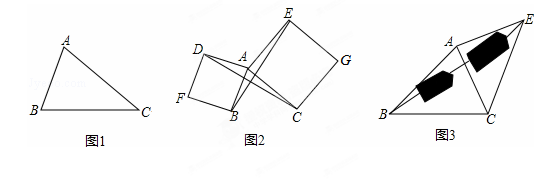

如图所示的4×4正方形网格中，∠1+∠2+∠3+∠4+∠5+∠6+∠7=（ ）

A．330°

B．315°

C．310°

D．320°

如图，为6个边长相等的正方形的组合图形，则∠1+∠2+∠3=         ．

如图，是由四个直角边分别为3和4且全等的直角三角形拼成的“赵爽弦图”，那么阴影部分面积为      ．

如图，某市有一块长为（3a+b）米，宽为（2a+b）米的长方形地块，规划部门计划将阴影部分进行绿化，中间将修建一座雕像，则绿化的面积是多少平方米？并求出当a=3，b=2时的绿化面积．

一个多边形的内角和是外角和的2倍，则这个多边形的边数为      ．

（10） 如图，在△ABC中，AD是∠BAC的平分线，EF垂直平分AD交AB于E，交AC于F．求证：四边形AEDF是菱形．

如图，菱形ABCD中，∠BAD=60º ，M是AB的中点，P是对角线AC上的一个动点，若AB长是3，则PM +PB的最小值为         ．

菱形的两条对角线的长分别是6和8 ，则这个菱形的周长是（   ）
A 24           B．20          C．10       D．5

如图，菱形ABCD中，∠B＝60°，AB＝2，E、F分别是BC、CD的中点，连接AE、EF、AF，则△AEF的周长为（   ）

A．        B．      C．       D．  

一块长方形草地的长和宽分别为20m和15m，在它四周外围环绕着宽度相等的小路，已知小路的面积为246㎡，求小路的宽度。

在△ABC中，中线BE、CF交于点O，M、N分别是BO、CO中点，则四边形MNEF是什么特殊四边形？并说明理由

菱形两对角线长分别为24和10，则这个菱形的面积是________，菱形的高为_____．

在一幅长80cm，宽50cm的长方形风景画的四周镶一条金色纸边（如图所示），制成一幅长方形挂图．如果要使整个挂图的面积是5400cm²，设金色纸边的宽为xcm，则由题意列方程得                       ．