初中数学圆内接四边形的性质试题

如图所示，正方形ABCD的边长为1，G为CD边上的一个动点（点G与C、D不重合），以CG为一边向正方形ABCD外作正方形GCEF，连接DE交BG的延长线于H．

求证：△BCG≌△DCE；
（1）求证：BH⊥DE；
（2）试问当CG等于多少时，BH垂直平分DE？

如图，把矩形纸片ABCD沿EF折叠，使点B落在边AD上的点D处，点A落在点处，连结BE．

求证：四边形是菱形；
若AB =" 4" cm，BC =" 8" cm，求折痕EF的长．

如图，△ABC中，AB = AC，AD、AE分别是∠BAC和∠BAC外角的平分线，．

（1）求证：DA⊥AE；
（2）试判断AB与DE是否相等？并证明你的结论．

如图所示，在□ABCD中，E、F是对角线AC上两点，且AE = CF．求证：四边形DEBF是平行四边形．

如图，已知□ABCD中，，DE⊥BC于E，BF⊥CD于F，DE、BF相交于H，BF、AD的延长线相交于G，下列结论：

①；②；③AB = BH；④；⑤BH = HG．
其中正确的结论有_________________（填上正确结论的序号）．

如图，在菱形ABCD中，，AB =" 4" cm．那么，菱形ABCD的对角线AC的长为_____cm

如图，已知平行四边形ABCD中，AE⊥BC，AF⊥DC，BC∶CD = 3∶2，AB = EC，则∠EAF=（ ）

A．45°

B．50°

C．60°

D．65°

如图，，，，下面的四个结论中：
①AB = CD； ②BE = CF；③；④，其中正确的有（   ）

A．4个

B．3个

C．2个

D．1个

如图，在梯形ABCD中，AD∥BC，AB = CD，，BD平分，如果这个梯形的周长为30，则AB的长为（   ）

A．4

B．5

C．6

D．7

矩形的两条对角线的夹角为60°，这个矩形较短边与对角线的比是（   ）

A．1∶1

B．1∶2

C．2∶3

D．1∶

.已知点C是AB的黄金分割点(AC >BC)，若AB=4cm，则AC的长为（    ）
A、2（-1）cm     B、cm
C.cm           D、cm

如图，A，B是公路l（l为东西走向）两旁的两个村庄，A村到公路l的距离AC=1km，B村到公路l的距离BD=2km，B村在A村的南偏东45°方向上．

（1）求出A，B两村之间的距离；
（2）为方便村民出行，计划在公路边新建一个公共汽车站P，要求该站到两村的距离相等，请用尺规在图中作出点P的位置（不写作法，保留清晰的作图痕迹）．

如图２，在菱形ABCD中，对角线AC=4，∠BAD=120°，则菱形ABCD的周长为

A．20

B．18

C．16

D．15

已知，如图，在平行四边形ABCD中，AE是BC边上的高，将△ABE沿BC方向平移，使点E与点C重合，得△GFC.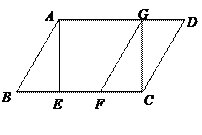

(1)求证：BE=DG；
(2)∠若B=60°，当AB与BC满足什么数量关系时，四边形ABFG是菱形？证明你的结论.

有一水库大坝的横截面是梯形ABCD，AD∥BC，EF为水库的水面，点E在DC上，某课题小组在老师带领下想测量水的深度，他们测得背水坡AB的长为12米，迎水坡DE的长为2米，∠BAD=135°，∠ADC=120°，求水深.（精确到0.1米，）