如图,四边形ABCD、DEFG都是正方形,连接AE、CG、AE与CG相交于点M,CG与AD相交于点N.
求证:(1) ;
;
(2)
设边长为2a的正方形的中心A在直线l上,它的一组对边垂直于直线l,半径为r的圆的圆心O在直线l上运动,A、O两点之间的距离为d.
(1)如图①,当r<a时,填表:
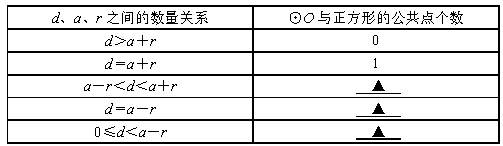
(2)如图②,⊙O与正方形有5个公共点B、C、D、E、F,求此时r与a之间的数量关系;
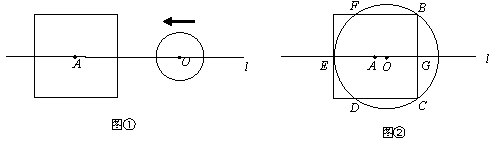
(3)由(1)可知,d、a、r之间的数量关系和⊙O与正方形的公共点个数密切相关.当r=a时,请根据d、a、r之间的数量关系,判断⊙O与正方形的公共点个数;
(4)当r与a之间满足(2)中的数量关系时,⊙O与正方形的公共点个数为 .
如图,矩形ABCD中,E为BC上一点,DF⊥AE于F.
(1)ΔABE与ΔADF相似吗?请说明理由.
(2)若AB=6,AD=12,BE=8,求FD的长.
如图,在直角梯形ABCD中,AD∥BC,∠B=90°,且AD=12cm,AB=8cm,DC=10cm,若动点P从A点出发,以每秒2cm的速度沿线段AD向点D运动;动点Q从C点出发以每秒3cm的速度沿CB向B点运动,当P点到达D点时,动点P、Q同时停止运动,设点P、Q同时出发,并运动了t秒,回答下列问题:

(1)BC= cm;
(2)当t为多少时,四边形PQCD成为平行四边形?
(3)当t为多少时,四边形PQCD为等腰梯形?
(4)是否存在t,使得△DQC是等腰三角形?若存在,请求出t的值;若不存在,说明理由.
如果一个正多边形的内角和是1440°,则这个正多边形是正边形。
如图,把一个长方形的纸片按图示对折两次,然后剪下一部分,为了得到一个钝角为120°的菱形,剪口与第二次折痕所成角的度数应为( )

| A.15°或30° | B.30°或45° | C.45°或60° | D.30°或60° |
如图,在矩形ABCD中,对角线 与
与 相交于点O,且AB=OA=2cm
相交于点O,且AB=OA=2cm  ,则BD的长为________cm,BC的长为_______cm.
,则BD的长为________cm,BC的长为_______cm.

以下说法错误的是
| A. |
多边形的内角大于任何一个外角 |
| B. |
任意多边形的外角和是 |
| C. |
正六边形是中心对称图形 |
| D. |
圆内接四边形的对角互补 |
下列命题中,正确的是( )
| A.四边相等的四边形是正方形 |
| B.四角相等的四边形是正方形 |
| C.对角线相等的菱形是正方形 |
| D.对角线垂直且相等的四边形是正方形 |
一个多边形的内角和是900°,则这个多边形的边数为( )
| A.6 | B.7 | C.8 | D.9 |
如图,平行四边形ABCD中,AE平分∠BAD交BC边于E,EF⊥AE交CD边于F,延长BA到点G,使AG=CF,连接GF.若BC=7,DF=3,tan∠AEB=3,则GF的长为 .
