初中数学圆内接四边形的性质试题

如果一个多边形的内角和是其外角和的2倍，那么这个多边形是（   ）．

A．六边形

B．五边形

C．四边形

D．三角形

如图，沿AE折叠矩形纸片ABCD，使点D落在BC边的点F处．已知AB=8，BC=10，则tan∠EFC的值为 （   ）

A．

B．

C．

D．

已知：如图，菱形ABCD中，对角线AC，BD相交于点O，且AC=12cm，BD=16cm．点P从点B出发，沿BA方向匀速运动，速度为1cm/s；同时，直线EF从点D出发，沿DB方向匀速运动，速度为1cm/s，EF⊥BD，且与AD，BD，CD分别交于点E，Q，F；当直线EF停止运动时，点P也停止运动．连接PF，设运动时间为t（s）（0＜t＜8）．解答下列问题：

（1）当t为何值时，四边形APFD是平行四边形？
（2）设四边形APFE的面积为y（cm²），求y与t之间的函数关系式；
（3）是否存在某一时刻t，使S_{四边形APFE}：S_菱形ABCD=17：40？若存在，求出t的值，并求出此时P，E两点间的距离；若不存在，请说明理由．

如图，已知四边形 $\mathit{ABCD}$ 是圆 $O$ 的内接四边形， $\angle \mathit{BOD}=80°$ ，则 $\angle \mathit{BCD}=$ 　　．

对于边长为3的正方形ABCD，建立适当的直角坐标系，写出各个顶点的坐标．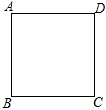

如图，四边形ABCD、DEFG都是正方形，连接AE、CG、AE与CG相交于点M，CG与AD相交于点N．

求证：（1）；
（2）

如图，矩形ABCD中，E为BC上一点，DF⊥AE于F．

（1）ΔABE与ΔADF相似吗？请说明理由．
（2）若AB=6，AD=12，BE=8，求FD的长．

如果一个正多边形的内角和是1440°，则这个正多边形是正边形。

顺次连结等腰梯形各边中点，所得的四边形一定是（   ）．

A．矩形

B．菱形

C．正方形

D．梯形

如图，在矩形ABCD中，对角线与相交于点O，且AB=OA=2cm ，则BD的长为________cm，BC的长为_______cm．

如图，在 $\odot O$ 内接四边形 $\mathit{ABCD}$ 中，若 $\angle \mathit{ABC}=100°$ ，则 $\angle \mathit{ADC}=$ 　　 $°$ ．

以下说法错误的是 $($ 　　 $)$

A．	多边形的内角大于任何一个外角
B．	任意多边形的外角和是 $360°$
C．	正六边形是中心对称图形
D．	圆内接四边形的对角互补

下列命题中，正确的是（     ）

A．四边相等的四边形是正方形

B．四角相等的四边形是正方形

C．对角线相等的菱形是正方形

D．对角线垂直且相等的四边形是正方形

一个多边形的内角和是900°，则这个多边形的边数为（ ）

A．6

B．7

C．8

D．9

如图，平行四边形ABCD中，AE平分∠BAD交BC边于E，EF⊥AE交CD边于F，延长BA到点G，使AG=CF，连接GF．若BC=7，DF=3，tan∠AEB=3，则GF的长为       ．