如图,如果边长为1的等边△PQR沿着边长为1的正方形ABCD的外部的边如图位置开始顺时针连续滚动,当它滚动121次时,点P所经过的路程是_________.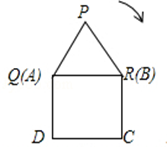
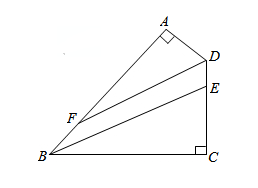
(10分)如图,四边形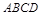 中,
中,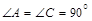 ,
,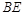 平分
平分 交
交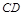 于
于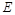 ,
,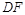 平分
平分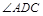 交
交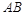 于
于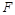 .
.
(1)若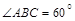 ,则
,则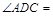 °,
°,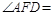 °;
°;
(2)求证:BE∥DF
如图,平行四边形ABCD中,AB=3,BC=5,AC的垂直平分线交AD于E,则△CDE的周长是( )

| A.6 | B.8 | C.9 | D.10 |
如图,在△ABC中,AB=BC,AB=12 cm,F是AB边上一点,过点F作FE∥BC交AC于点E,过点E作ED∥AB交BC于点D,则四边形BDEF的周长是 .
如图,在长为100m,宽为80 m的矩形场地上修建两条宽度相等且互相垂直的道路,剩余部分进行绿化,要使绿化面积为7644m2,则道路的宽应为多少米?设道路的宽为x m,则可列方程为 ( )

| A.100×80-100x-80x="7644" | B.(100-x)(80-x)+x2="7644" |
| C.(100-x)(80-x)="7644" | D.100x+80x-x2=7644 |
如图3,在平面直角坐标系中,第一象限内长方形ABCD,AD∥x轴,点E在x轴上,EC交AD于G, BF平分∠CBE交OC于F,若∠CGD=2∠OCE,则下列结论正确的是( ).
| A.∠BEC=∠BFO |
| B.∠BEC+∠BFO=1350 |
C. ∠BEC+∠BFO= 900 ∠BEC+∠BFO= 900 |
D.∠BEC+ ∠BFO= 900 ∠BFO= 900 |
如图,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为( )

| A.1 | B. |
C.2 | D. |
如图,四边形 是 的内接四边形, 是 的直径,连接 .若 ,则 的度数是

| A. |
|
B. |
|
C. |
|
D. |
|
如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.若AB=8,AD=6 ,AF=4
,AF=4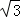 ,则AE的长为 .
,则AE的长为 .
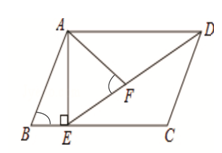
一个正方形和两个等边三角形的位置如图所示,若∠3=50°,则∠1+∠2=( )

| A.90° | B.100° | C.130° | D.180° |
如图,在四边形ABCD中,已知AB∥DC,AB=DC.在不添加任何辅助线的前提下,要想该四边形成为矩形,只需再加上的一个条件是 .(填上你认为正确的一个答案即可)