下列说法正确的是( )
| A.顺次连接矩形各边中点的四边形一定也是矩形 |
| B.对角线互相垂直的四边形是菱形 |
| C.有一个角是直角的菱形一定是正方形 |
| D.平行四边形的对角线相等且互相平分 |
如图,点P是菱形ABCD内一点,PE⊥AB,PF⊥AD,垂足分别是E和F,若PE=PF,下列说法不正确的是( )

| A.点P一定在菱形ABCD的对角线AC上 |
| B.可用HL证明Rt△AEP≌Rt△AFP |
| C.AP平分∠BAD |
| D.点P一定是菱形ABCD的两条对角线的交点 |
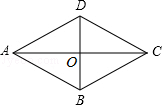
如图,菱形ABCD的两条对角线相交于O,若AC=6,BD=4,则菱形ABCD的周长是 .
如图,平行四边形ABCD中,AB=3,BC=5,AC的垂直平分线交AD于E,则△CDE的周长是( )

| A.6 | B.8 | C.9 | D.10 |
一个正方形和四个全等的小正方形按图①②两种方式摆放,若把图②中未被小正方形覆盖部分(图②中的阴影部分)折成一个无盖的长方体盒子,则此长方体盒子的体积为( )

A. |
B. |
C. |
D. |
如图,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为( )

| A.1 | B. |
C.2 | D. |
如图,一个多边形纸片按图示的剪法剪去一个内角后,得到一个内角和为2340°的新多边形,则原多边形的边数为( )

| A.13 | B.14 | C.15 | D.16 |
矩形、菱形、正方形都是特殊的四边形,它们具有很多共性,如: .(填一条即可)
如图,已知在矩形ABCD中,AB=4,BC=2,点M,E在AD上,点F在边AB上,并且DM=1,现将△AEF沿着直线EF折叠,使点A落在边CD上的点P处,则当PB+PM的和最小时,ME的长度为( )

A. |
B. |
C. |
D. |
平行四边形ABCD与等边△AEF如图放置,如果∠B=45°,则∠BAE的大小是( )
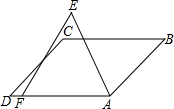
| A.75° | B.70° | C.65° | D.60° |
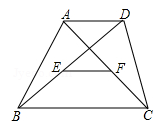
如图,在梯形ABCD中,AD∥BC,E,F分别是对角线BD、AC的中点,AD=22cm,BC=38cm,则EF= .
如图,在菱形ABCD中,AB=1,∠DAB=60°,把菱形ABCD绕点A顺时针旋转30°得到菱形AB′C′D′,其中点C的运动路径为 ,则图中阴影部分的面积为 .
,则图中阴影部分的面积为 .

如图,菱形ABCD的对角线AC,BD相交于点O,AC=8,BD=6,以AB为直径作一个半圆,则图中阴影部分的面积为( )

| A.25π-6 | B. π-6 π-6 |
C. π-6 π-6 |
D. π-6 π-6 |
若一个多边形的内角和90 0°,则这个多边形的边数为( )
| A.5 | B.7 | C.9 | D.12 |