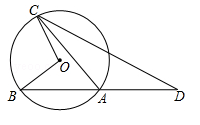
如图,为
的直径,
为
延长线上一点,
是
的切线,
为切点,
于点
,交
于点
.
(1)求证:;
(2)若,
,求
的长.
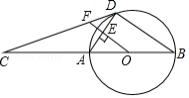
已知:如图, 为锐角三角形, , .
求作:线段 ,使得点 在直线 上,且 .
作法:①以点 为圆心, 长为半径画圆,交直线 于 , 两点;
②连接 .
线段 就是所求作的线段.
(1)使用直尺和圆规,依作法补全图形(保留作图痕迹);
(2)完成下面的证明.
证明: ,
.
,
点 在 上.
又 点 , 都在 上,
(填推理的依据).
.

如图,A、B、C、D四个点均在⊙O上,∠AOD=70°,AO∥DC,则∠B的度数为( )

A.40° B.45° C.50° D.55°
如图,将直角三角板45°角的顶点放在圆心O上,斜边和一直角边分别与⊙O相交于A、B两点,C是优弧AB上任意一点(与A、B不重合),则∠ACB的度数是( )

A.30o B.22.5o C.90o D.15o
如图,已知⊙O是△ABD的外接圆,AB是⊙O的直径,CD是⊙O的弦,∠ABD=58°,则∠BCD等于( )
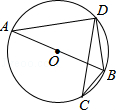
| A.116° | B.32° | C.58° | D.64° |
如图,△ABC内接于⊙O,∠B=60º,∠A=40º,半径OE⊥AB,连接CE,则∠E=( )

| A.5º | B.10º | C.15º | D.20º |
在△ABC中,BC =4,以点A为圆心、2为半径的⊙A与BC相切于点D,交AB于E,交 AC于F,点P是⊙A上的一点,且∠EPF=40°,则图中阴影部分的面积是( )
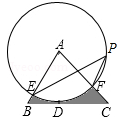
A.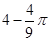 |
B.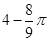 |
C. |
D.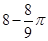 |
如图,线段AB是⊙O的直径,弦CD丄AB,∠CAB=20°,则∠AOD等于( )
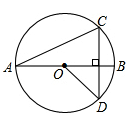
| A.120° | B.140° | C.150° | D.160° |
如图,线段AB是⊙O的直径,弦CD丄AB,∠CAB=20°,则∠AOD等于( )
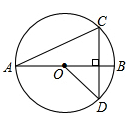
| A.120° | B.140° | C.150° | D.160° |
(年云南省)如图,点A,B,C是⊙O上的点,OA=AB,则∠C的度数为 .
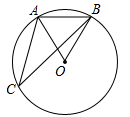
(年江西省南昌市)如图,点A,B,C在⊙O上,CO的延长线交AB于点D,∠A=50°,∠B=30°,则∠ADC的度数为 .
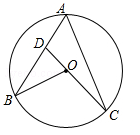
(年云南省曲靖市)如图,在半径为3的⊙O中,直径AB与弦CD相交于点E,连接AC,BD,若AC=2,则cosD= .
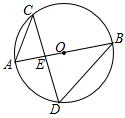
(年青海省中考)如图,点O为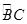 所在圆的圆心,∠BOC=112°,点D在BA的延长线上,AD=AC,则∠D= .
所在圆的圆心,∠BOC=112°,点D在BA的延长线上,AD=AC,则∠D= .