初中数学圆填空题

如图中，由一个直角三角形和两个正方形组成，如果大正方形的面积为41，AB=5，则小正方形的面积为____________．

如图，在正方形ABCD中，点F为CD上一点，BF与AC交于点E．若∠CBF=20°，则∠AED等于     度．

如图1，点E为正方形ABCD的边AB上一点，EF⊥EC，且EF=EC，连接AF．
（1）求∠FAD的度数；
（2）如图2，连接FC交BD于M，求证：AD=AF+2DM；
（3）如图2，连接FC交BD于M，交AD于N．若AF=，AN=10，则BM的长为              ．

把矩形ABCD沿着CE折叠，使得点F落在AD上，若AB＝8，BC＝10，则折痕线CE＝_________．

若菱形的周长为8，相邻两内角之比为3：1，则菱形的高是    ．

如图，在菱形ABCD中，AB=10，AC=12，则它的面积是       ．

如图，菱形ABCD的对角线AC，BD相交于点O，分别延长OA，OC到点E，F，使AE=CF，依次连接B，F，D，E各点．

（1）求证：△BAE≌△BCF；
（2）若∠ABC=50°，则当∠EBA=       °时，四边形BFDE是正方形．

一个n边形的内角和是720°，那么n＝        ．

如图，正方形ABCD的边长为1，中心为点O，有一边长大小不定的正六边形EFGHIJ绕点O可任意旋转，在旋转过程中，这个正六边形始终在正方形ABCD内（包括正方形的边），当这个六边形的边长最大时，AE的最小值为              ．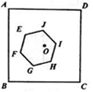

如图，在矩形ABCD中，AB=，AD=10，连接BD，DBC的角平分线BE交DC于点E，现把△BCE绕点B逆时针旋转，记旋转后的△BCE为△．当射线和射线都与线段AD相交时，设交点分别F，G．若△BFD为等腰三角形，则线段DG长为               ．
      

如图，已知正方形ABCD边长为3，点E在AB边上且BE=1，点P，Q分别是边BC，CD的动点（均不与顶点重合），当四边形AEPQ的周长取最小值时，四边形AEPQ的面积是     ．

如图，在菱形ABCD中，AB=6，∠DAB=60°，AE分别交BC、BD于点E、F，CE=2，连接CF，以下结论：①△ABF≌△CBF；②点E到AB的距离是2 ；③tan∠DCF= ；④△ABF的面积为．其中一定成立的是           （把所有正确结论的序号都填在横线上）．

一个边形的内角和比它的外角和至少大，则的最小值是          ．

若一个多边形内角和为900°，则这个多边形是     边形．

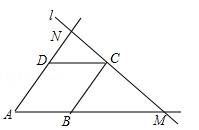
如图，菱形ABCD的边长为1，直线l过点C，交AB的延长线于M，交AD的延长线于N，则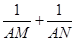=    ．