初中数学圆选择题

如图，正方形ABCD的边长为4，点P、Q分别是CD、AD的中点，动点E从点A向点B运动，到点B时停止运动；同时，动点F从点P出发，沿P→D→Q运动，点E、F的运动速度相同．设点E的运动路程为x，△AEF的面积为y，能大致刻画y与x的函数关系的图象是（ ）

A．  B．  C．  D．

如果一个多边形的每一个外角都是60°，则这个多边形的边数是（ ）
A．3          B，4           C.5              D.6

一个多边形的每个内角均为120°，则这个多边形是（  ）

A．四边形

B．五边形

C．六边形

D．七边形

将一块正方形铁皮的四角各剪去一个边长为3cm的小正方形，做成一个无盖的盒子，已知盒子的容积为300 ，则原铁皮的边长为（ ）

A．10cm

B．13cm

C．14cm

D．16cm

如图，在Rt△ABC中，∠C=90°。若AB=15，则正方形ADEC和正方形BCFG的面积和为（  ）

A．150

B．200

C．225

D．无法计算

四边形ABCD中，对角线AC与BD交于点O，下列条件不能判定这个四边形是平行四边形的是（  ）

A．OA=OC，OB=OD

B．AD∥BC，AB∥DC

C．AB=DC，AD=BC

D．AB∥DC，AD=BC

如图，G，E分别是正方形ABCD的边AB，BC的点，且AG=CE，AE⊥EF，AE=EF，现有如下结论：①BE=GE；②△AGE≌△ECF；③∠FCD=45°；④△GBE∽△ECH
其中，正确的结论有（ ）

A．1个

B．2个

C．3个

D．4个

下列命题中，属于真命题的是（ ）

A．各边相等的多边形是正多边形

B．矩形的对角线互相垂直

C．三角形的中位线把三角形分成面积相等的两部分

D．对顶角相等

下列多边形中，内角和与外角和相等的是（  ）

A．四边形

B．五边形

C．六边形

D．八边形

在□ABCD中，如果∠A+∠C＝140°，那么∠C等于（      ）．

A．20°

B．40°

C．60°

D．70°

如图，在菱形ABCD中，对角线AC、BD相交于点O，下列结论：①AC⊥BD；②OA=OB；③∠ADB=∠CDB；④△ABC是等边三角形，其中一定成立的是（ ）

A．①②      B．③④      C．②③      D．①③

如图，已知AB=AC=AD，∠CBD=2∠BDC，∠BAC=44°，则∠CAD的度数为（ ）

A．68°

B．88°

C．90°

D．112°

如图所示，正方形ABCD的对角线AC，BD相交于点O，DE平分∠ODC交OC于点E，若AB=2，则线段OE的长为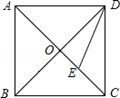

A．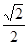

B．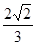

C．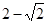

D．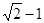

如图，点P是在□ABCD边上一动点，沿A→D→C→B的路径移动，设P点经过的路径长为x，△BAP的面积是y，则下列能大致反映y与x的函数关系的图象是

正六边形的每一个外角都是（  ）．

A．

B．

C．

D．