初中数学圆试题

（11·佛山）在矩形ABCD中，两条对角线AC、BD相交于点O，若AB＝OB＝4，则AD＝ ；

（11·佛山）依次连接菱形的各边中点，得到的四边形是（              ）

A．矩形

B．菱形

C．正方形

D．梯形

如图，在□ABCD中，AC、BD相交于点O，点E是AB的中点．若OE＝3cm，则AD的长是       cm．

矩形、菱形、正方形都是平行四边形，但它们都是有特殊条件的平行四边形，正方形不仅是特殊的矩形，也是特殊的菱形.因此，我们可利用矩形、菱形的性质来研究正方形的有关问题.回答下列问题：
（1）将平行四边形、矩形、菱形、正方形填入它们的包含关系的下图中.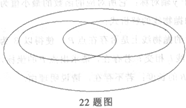

（2）要证明一个四边形是正方形，可先证明四边形是矩形，再证明这个矩形的_______相等；或者先证明四边形是菱形，在证明这个菱形有一个角是________ .
（3）某同学根据菱形面积计算公式推导出对角线长为a的正方形面积是S=0.5a²，对此结论，你认为是否正确？若正确，请说明理由；若不正确，请举出一个反例说明.

在Rt△ABC中，∠C=90°，AC=3，BC=4，将△ABC绕边AC所在直线旋转一周得到圆锥，则该圆锥的侧面积是___________.

如图，D，E，F分别为△ABC三边的中点，则图中平行四边形的个数为　．

以四边形ABCD的边AB、BC、CD、DA为斜边分别向外侧作等腰直角三角形，直角顶点分别为E、F、G、H，顺次连接这四个点，得四边形EFGH．
（1）如图1，当四边形ABCD为正方形时，我们发现四边形EFGH是正方形；如图2，当四边形ABCD为矩形时，请判断：四边形EFGH的形状（不要求证明）；
（2）如图3，当四边形ABCD为一般平行四边形时，设∠ADC=α（0°＜α＜90°），
①试用含α的代数式表示∠HAE；
②求证：HE=HG；
③四边形EFGH是什么四边形？并说明理由．

如图，①②③④⑤五个平行四边形拼成一个含30°内角的菱形EFGH（不重叠无缝隙）．若①②③④四个平行四边形面积的和为14cm²，四边形ABCD面积是11cm²，则①②③④四个平行四边形周长的总和为（　　）

A．48cm	B．36cm
C．24cm	D．18cm

(本题8分)如图，射线PG平分∠EPF，O为射线PG上一点，以O为圆心，10为半径作⊙O，分别与∠EPF的两边相交于A、B和C、D，连结OA，此时有OA//PE．
（1）求证：AP=AO；
（2）若tan∠OPB=，求弦AB的长；
（3）若以图中已标明的点（即P、A、B、C、D、O）构造四边形，则能构成菱形的四个点为 ▲ ，能构成等腰梯形的四个点为 ▲ 或 ▲ 或 ▲ .

如图,在□ABCD中，AB=3，AD=4，∠ABC=60°，过BC的中点E作EF⊥AB，垂足为点F，与DC的延长线相交于点H，则△DEF的面积是 ▲ .

如图6，已知菱形ABCD，其顶点A、B在数轴上对应的数分别为－4和1，则
BC=_____.

（本小题满分9分）如图12，四边形ABCD是正方形，点E，K分别在BC，AB
上，点G在BA的延长线上，且CE=BK=AG.
⑴求证：①DE=DG；②DE⊥DG；
⑵尺规作图：以线段DE，DG为边作出正方形DEFG（要求：只保留作图痕迹，不写作法和证明）；
⑶连接⑵中的KF，猜想并写出四边形CEFK是怎样的特殊四边形，并证明你的猜想；
⑷当时，请直接写出的值.

（本题满分12分，每小题满分各6分）如图，在梯形ABCD中，AD//BC，AB＝DC，过点D作DE⊥BC，垂足为E，并延长DE至F，使EF＝DE．联结BF、CD、AC．
（1）求证：四边形ABFC是平行四边形；
（2）如果DE²＝BE·CE，求证四边形ABFC是矩形．

如图1，AM是△ABC的中线，设向量，，那么向量____________（结果用、表示）．

（本小题满分8分）在正方形ABCD的边AB上任取一点E，作EF⊥AB交BD于点F，取FD的中点G，连结EG、CG，如图（1），易证 EG=CG且EG⊥CG.
（1）将△BEF绕点B逆时针旋转90°，如图（2），则线段EG和CG有怎样的数量关系和
位置关系？请直接写出你的猜想.
（2）将△BEF绕点B逆时针旋转180°，如图（3），则线段EG和CG又有怎样的数量关系
和位置关系？请写出你的猜想，并加以证明.