已知:如图,在▱ABCD中,O为对角线BD的中点,过点O的直线EF分别交AD,BC于E,F两点,连结BE,DF.
(1)求证:△DOE≌△BOF;
(2)当∠DOE等于多少度时,四边形BFDE为菱形?请说明理由.
已知矩形OABC中,OA=3,AB=6,以OA、OC所在的直线为坐标轴,建立如图所示的平面直角坐标系.将矩形OABC绕点O顺时针方向旋转,得到矩形ODEF,当点B在直线DE上时,设直线DE和x轴交于点P,与y轴交于点Q.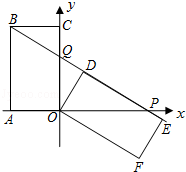
(1)求证:△BCQ≌△ODQ;
(2)求点P的坐标.
如图,在矩形ABCD中,点E是边CD的中点,将△ADE沿AE折叠后得到△AFE,且点F在矩形ABCD内部.将AF延长交边BC于点G.若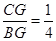 ,则
,则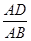 =( )
=( )
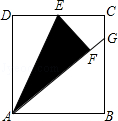
A.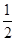 |
B.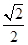 |
C. |
D.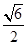 |
若一个多边形的内角和等于720°,则这个多边形的边数是( )
| A.5 | B.6 | C.7 | D.8 |
下列命题是假命题的是( )
| A.对角线互相平分的四边形是平行四边形 |
| B.对角线互相垂直的四边形是菱形 |
| C.对角线相等的平行四边形是矩形 |
| D.对角线相等的菱形是正方形 |
如图,将边长为8的正方形纸片ABCD折叠,使点B落在CD边的中点E上,压平后得到折痕MN,EF与AD边交于点G.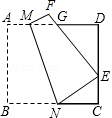
(1)求CN的长;
(2)求DG的长;
(3)AM= .(直接填结果)
如图,在平行四边形ABCD中,若AB=6,AD=10,∠ABC的平分线交AD于点E,交CD的延长线于点F,求DF的长.
如图,矩形ABCD中,AB=8,AD=6,点E、F分别在边CD、AB上.
(1)若DE=BF,求证:四边形AFCE是平行四边形;
(2)若四边形AFCE是菱形,求菱形AFCE的周长.
如图,边长为1的正方形ABCD,点M从点A出发以每秒1个单位长度的速度向点B运动,点N从点A出发以每秒3个单位长度的速度沿A→D→C→B的路径向点B运动,当一个点到达点B时,另一个点也随之停止运动,设△AMN的面积为s,运动时间为t秒,则能大致反映s与t的函数关系的图象是( )
A. |
B. |
C. |
D. |
如图,折叠矩形OABC的一边BC,使点C落在OA边的点D处,已知折痕BE=5 ,且
,且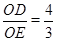 ,以O为原点,OA所在的直线为x轴建立如图所示的平面直角坐标系,抛物线l:y=-
,以O为原点,OA所在的直线为x轴建立如图所示的平面直角坐标系,抛物线l:y=- +c经过点E,且与AB边相交于点F.
+c经过点E,且与AB边相交于点F.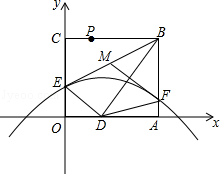
(1)求证:△ABD∽△ODE;
(2)若M是BE的中点,连接MF,求证:MF⊥BD;
(3)P是线段BC上一点,点Q在抛物线l上,且始终满足PD⊥DQ,在点P运动过程中,能否使得PD=DQ?若能,求出所有符合条件的Q点坐标;若不能,请说明理由.
如图,在△ABC中,CD是AB边上的中线,F是CD的中点,过点C作AB的平行线交BF的延长线于点E,连接AE.
(1)求证:EC=DA;
(2)若AC⊥CB,试判断四边形AECD的形状,并证明你的结论.
如图,小明从A点出发,沿直线前进12米后向左转36°,再沿直线前进12米,又向左转36°…照这样走下去,他第一次回到出发地A点时,一共走了 米.
如图,P为平行四边形ABCD的边AD上的一点,E,F分别为PB,PC的中点,△PEF,△PDC,△PAB的面积分别为S, ,
, .若S=3,则
.若S=3,则 的值为( )
的值为( )
| A.24 | B.12 | C.6 | D.3 |