初中数学圆试题

图①，图②，图③都是4×4的正方形网格，每个小正方形的顶点称为格点，每个小正方形的边长均为1．在图①，图②中已画出线段AB，在图③中已画出点A．按下列要求画图：

（1）在图①中，以格点为顶点，AB为一边画一个等腰三角形；
（2）在图②中，以格点为顶点，AB为一边画一个正方形；
（3）在图③中，以点A为一个顶点，另外三个顶点也在格点上，画一个面积最大的正方形．

如图，在▱ABCD中，AE⊥BC，交边BC于点E，点F为边CD上一点，且DF=BE．过点F作FG⊥CD，交边AD于点G．求证：DG=DC．

如图，在菱形ABCD中，点A在x轴上，点B的坐标为（8，2），点D的坐标为（0，2），则点C的坐标为             ．

如图，正方形ABCD和正△AEF都内接于⊙O，EF与BC、CD分别相交于点G、H，则的值是（ ）

A．      B．      C．      D．2

如图，AB是⊙O的直径，OB=3，BC是⊙O的弦，∠ABC的平分线交⊙O于点D，连接OD，若∠BAC=20°，则的长等于         ．

如图，在矩形ABCD中，∠BAD的平分线交BC于点E，交DC的延长线于点F，取EF的中点G，连接CG，BG，BD，DG，下列结论：

①BE=CD；
②∠DGF=135°；
③∠ABG+∠ADG=180°；
④若，则．
其中正确的结论是        ．（填写所有正确结论的序号）

如图，在边长为的菱形ABCD中，∠A=60°，点E，F分别在AB，AD上，沿EF折叠菱形，使点A落在BC边上的点G处，且EG⊥BD于点M，则EG的长为    ．

如图，点E是▱ABCD的边AD的中点，连接CE交BD于点F，如果S_△DEF=a，那么S_△BCF=       ．

已知四边形ABCD是正方形，等腰直角△AEF的直角顶点E在直线BC上（不与点B，C重合），FM⊥AD，交射线AD于点M．

（1）当点E在边BC上，点M在边AD的延长线上时，如图①，求证：AB+BE=AM；
（提示：延长MF，交边BC的延长线于点H．）
（2）当点E在边CB的延长线上，点M在边AD上时，如图②；当点E在边BC的延长线上，点M在边AD上时，如图③．请分别写出线段AB，BE，AM之间的数量关系，不需要证明；
（3）在（1），（2）的条件下，若BE=，∠AFM=15°，则AM=     ．

如图，在矩形ABCD中，点E、F分别是边AB、CD的中点．求证：DE=BF．

如图，要使▱ABCD成为菱形，则需添加的一个条件是（ ）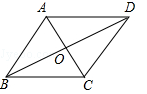

A．AC=AD

B．BA=BC

C．∠ABC=90°

D．AC=BD

如图，平行四边形ABCD的对角线AC、BD相交于点O，BC=9，AC=8，BD=14，则△AOD的周长为       ．

已知：如图①，在矩形ABCD中，AB=5，AD=，AE⊥BD，垂足是E．点F是点E关于AB的对称点，连接AF、BF．

（1）求AE和BE的长；
（2）若将△ABF沿着射线BD方向平移，设平移的距离为m（平移距离指点B沿BD方向所经过的线段长度）．当点F分别平移到线段AB．AD上时，直接写出相应的m的值．
（3）如图②，将△ABF绕点B顺时针旋转一个角α（0°＜α＜180°），记旋转中的△ABF为△A′BF′，在旋转过程中，设A′F′所在的直线与直线AD交于点P，与直线BD交于点Q．是否存在这样的P、Q两点，使△DPQ为等腰三角形？若存在，求出此时DQ的长；若不存在，请说明理由．

如图，菱形ABCD中，AB=2，∠A=120°，点P，Q，K分别为线段BC，CD，BD上的任意一点，则PK+QK的最小值为（ ）

A．1

B．

C．2

D．+1

△ABC中，AB=AC=10，BC=12，矩形DEFG中，EF=4，FG＞12．
（1）如图①，点A是FG的中点，FG∥BC，将矩形DEFG向下平移，直到DE与BC重合为止．要研究矩形DEFG与△ABC重叠部分的面积，就要进行分类讨论，你认为如何进行分类，写出你的分类方法（无需求重叠部分的面积）．
（2）如图②，点B与F重合，E、B．C在同一直线上，将矩形DEFG向右平移，直到点E与C重合为止．设矩形DEFG与△ABC重叠部分的面积为y，平移的距离为x．
①求y与x的函数关系式，并写出自变量的取值范围；
②在给定的平面直角坐标系中画出y与x的大致图象，并在图象上标注出关键点坐标．