初中数学圆试题

如图，在四边形ABCD中，E、F分别为对角线BD上的两点，且BE=DF．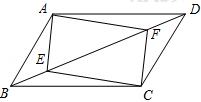

（1）若四边形AECF是平行四边形，求证：四边形ABCD是平行四边形；
（2）若四边形AECF是菱形，则四边形ABCD是菱形吗？请说明理由？
（3）若四边形AECF是矩形，则四边形ABCD是矩形吗？不必写出理由．

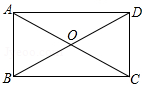
如图，矩形ABCD中，对角线AC、BD交于点O，若∠BOC=120°，AC=8，AB的长度是（   ）

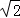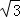A．4  B．4  C．4  D．8

菱形的周长为8cm，高为1cm，则该菱形两邻角度数比为（   ）

A．3：1

B．4：1

C．5：1

D．6：1

在下列性质中，平行四边形不一定具有的是（   ）

A．对边相等

B．对边平行

C．对角互补

D．内角和为360°

如图，在正方形ABCD中，CE⊥DF，求证：CE=DF．

菱形的两对条角线长分别为10cm、24cm，则它的周长为          cm．

如图，矩形ABCD中，BE、CF分别平分∠ABC和∠DCB，点E、F都在AD上，下列结论不正确的是(      )

A．△ABE≌△DCF

B．△ABE和△DCF都是等腰直角三角形

C．四边形BCFE是等腰梯形

D．E、F是AD的三等分点

已知▱ABCD中，若∠A+∠C=120°，则∠B的度数是（ ）

A．100°

B．120°

C．80°

D．60°

如图，平行四边形ABCD的两条对角线相交于点O，点E是AB边的中点，图中已有三角形与△ADE面积相等的三角形（不包括△ADE）共有（ ）个．

A．3

B．4

C．5

D．6

多边形的每个内角均为120°，则这个多边形的边数是（ ）

A．4

B．5

C．6

D．8

能判定一个四边形是平行四边形的条件是(   )

A．一组对边平行，另一组对边相等

B．一组对角相等，另一组对角互补

C．一组对角相等，一组邻角互补

D．一组对边平行，一组对角互补

如图，在直角坐标系中，矩形OABC的顶点O在坐标原点，边OA在x轴上，OC在y轴上，如果矩形OA′B′C′与矩形OABC关于点O位似，且矩形OA′B′C′的面积等于矩形OABC面积的，那么点B′的坐标是（ ）

A．（-2，3）	B．（2，-3）
C．（3，-2）或（-2，3）	D．（-2，3）或（2，-3）

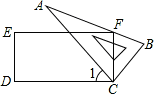
如图，把一块含有30°角（∠A=30°）的直角三角板ABC的直角顶点放在矩形桌面CDEF的一个顶点C处，桌面的另一个顶点F与三角板斜边相交于点F，如果∠1=40°，那么∠AFE=（ ）

A．50°

B．40°

C．20°

D．10°

（1）知识再现
如图（1）：若点A，B在直线l同侧，A，B到l的距离分别是3和2，AB=4，现在直线l上找一点P，使AP+BP的值最小，做法如下；
作点A关于直线l的对称点A′，连接BA′，与直线l的交代就是所求的点P，线段BA′的长度即为AP+BP的最小值，请你求出这个最小值．
（2）实践应用
①如图（2），⊙O的半径为2，点A、B、C在⊙O上，OA⊥OB，∠AOC=60°，P是OB上一动点，则PA+PC的最小值是               ；
②如图（3），Rt△OAB的顶点A在x轴的正半轴上，顶点B的坐标为（3，），点C的坐标为（1，0），点P为斜边OB上的一动点，则PA+PC的最小值为           ；
③如图（4），菱形ABCD中AB=2，∠A=120°，点P，Q，K，分别为线段BC，CD，BD上的任意一点，则PK+QK的最小值为             ；
④如图（5），在Rt△ABC中，∠C=90°，∠B=60°，点D是BC边上的点，CD=，将△ABC沿直线AD翻折，使点C落在AB边上的点E处，若点P是直线AD上的动点，则△PEB的周长的最小值是       ．
（3）拓展延伸
如图（6），在四边形ABCD的对角线AC上找一点P，使∠APB=∠APD，保留作图痕迹，不必写出作法．

在△ABC中，点D、E、F分别在BC、AB、CA上，且DE∥CA，DF∥BA，则下列三种说法：
①如果∠BAC=90°，那么四边形AEDF是矩形
②如果AD平分∠BAC，那么四边形AEDF是菱形
③如果AD⊥BC且AB=AC，那么四边形AEDF是菱形
其中正确的有（   ）

A.3个           B．2个          C.1个            D．0个