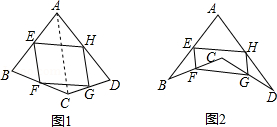
如图1,已知点 , , , 分别是四边形 各边 , , , 的中点,根据以下思路可以证明四边形 是平行四边形:
(1)如图2,将图1中的点 移动至与点 重合的位置, , , 仍是 , , 的中点,求证:四边形 是平行四边形;
(2)如图3,在边长为1的小正方形组成的 网格中,点 , , 都在格点上,在格点上画出点 ,使点 与 , , 的中点 , , 组成正方形 ;
(3)在(2)条件下求出正方形 的边长.
如图1,在四边形 中,如果对角线 和 相交并且相等,那么我们把这样的四边形称为等角线四边形.

(1)①在“平行四边形、矩形、菱形”中, 一定是等角线四边形(填写图形名称);
②若 、 、 、 分别是等角线四边形 四边 、 、 、 的中点,当对角线 、 还要满足 时,四边形 是正方形.
(2)如图2,已知 中, , , , 为平面内一点.
①若四边形 是等角线四边形,且 ,则四边形 的面积是 ;
②设点 是以 为圆心,1为半径的圆上的动点,若四边形 是等角线四边形,写出四边形 面积的最大值,并说明理由.
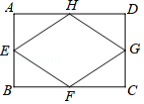
如图,在矩形 中,分别取 , , , 的中点 , , , ,连接 , , , ,求证:四边形 是菱形.
阅读下面材料:
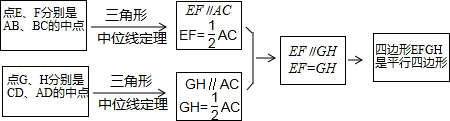
在数学课上,老师请同学思考如下问题:如图1,我们把一个四边形ABCD的四边中点E,F,G,H依次连接起来得到的四边形EFGH是平行四边形吗?
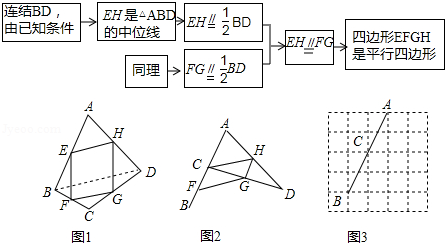
小敏在思考问题是,有如下思路:连接AC.
结合小敏的思路作答
(1)若只改变图1中四边形ABCD的形状(如图2),则四边形EFGH还是平行四边形吗?说明理由;参考小敏思考问题方法解决以下问题:
(2)如图2,在(1)的条件下,若连接AC,BD.
①当AC与BD满足什么条件时,四边形EFGH是菱形,写出结论并证明;
②当AC与BD满足什么条件时,四边形EFGH是矩形,直接写出结论.