初中数学三角形中位线定理试题

下面是小东设计的“过直线外一点作这条直线的平行线”的尺规作图过程．

已知：直线及直线外一点．

求作：直线，使得．

作法：如图，

①在直线上取一点，作射线，以点为圆心，长为半径画弧，交的延长线于点；

②在直线上取一点（不与点重合），作射线，以点为圆心，长为半径画弧，交的延长线于点；

③作直线．所以直线就是所求作的直线．

根据小东设计的尺规作图过程，

（1）使用直尺和圆规，补全图形；（保留作图痕迹）

（2）完成下面的证明．

证明：　　，　　，

　　（填推理的依据）．

如图，在中，、分别为，的中点．若，则　　．

如图，在四边形 $\mathit{ABCD}$ 中， $\angle \mathit{ABC}=90°$ ， $\mathit{AC}=\mathit{AD}$ ， $M$ ， $N$ 分别为 $\mathit{AC}$ ， $\mathit{CD}$ 的中点，连接 $\mathit{BM}$ ， $\mathit{MN}$ ， $\mathit{BN}$ ．

（1）求证： $\mathit{BM}=\mathit{MN}$ ；

（2） $\angle \mathit{BAD}=60°$ ， $\mathit{AC}$ 平分 $\angle \mathit{BAD}$ ， $\mathit{AC}=2$ ，求 $\mathit{BN}$ 的长．

在中，，，是的中点．为直线上一动点，连接．过点作，交直线于点，连接．

（1）如图1，当是线段的中点时，设，，求的长（用含，的式子表示）；

（2）当点在线段的延长线上时，依题意补全图2，用等式表示线段，，之间的数量关系，并证明．

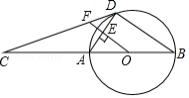
如图，为的直径，为延长线上一点，是的切线，为切点，于点，交于点．

（1）求证：；

（2）若，，求的长．

（年江西省南昌市）我们把两条中线互相垂直的三角形称为“称为中垂三角形”，例如图1，图2，图3中，AF，BE是△ABC的中线，AF⊥BE，垂足为P，像△ABC这样的三角形均称为“中垂三角形”，设BC=a，AC=b，AB=c．
特例探索
（1）如图1，当∠ABE=45°，c=时，a=       ，b=       ．
如图2，当∠ABE=30°，c=4时，a=       ，b=       ．
归纳证明
（2）请你观察（1）中的计算结果，猜想，，三者之间的关系，用等式表示出来，并利用图3证明你发现的关系式．
拓展应用
（3）如图4，在▱ABCD中，点E、F、G分别是AD，BC，CD的中点，BE⊥EG，AD=，AB=3，求AF的长．

（年贵州省铜仁市）如图，∠ACB=9O°，D为AB中点，连接DC并延长到点E，使CE=CD，过点B作BF∥DE交AE的延长线于点F．若BF=10，则AB的长为      ．

（年云南省）如图，在△ABC中，BC=1，点P₁，M₁分别是AB，AC边的中点，点P₂，M₂分别是AP₁，AM₁的中点，点P₃，M₃分别是AP₂，AM₂的中点，按这样的规律下去，P_nM_n的长为     （n为正整数）．

（年云南省昆明市）如图，在△ABC中，AB=8，点D、E分别是BC、CA的中点，连接DE，则DE=      ．

（年云南省昆明市）如图，△ABC是等边三角形，高AD、BE相交于点H，BC=，在BE上截取BG=2，以GE为边作等边三角形GEF，则△ABH与△GEF重叠（阴影）部分的面积为     ．