我国古代数学名著《孙子算经》有估算方法:“方五,邪(通“斜” 七.见方求邪,七之,五而一.”译文为:如果正方形的边长为五,则它的对角线长为七.已知正方形的边长,求对角线长,则先将边长乘以七再除以五.若正方形的边长为1,由勾股定理得对角线长为
,依据《孙子算经》的方法,则它的对角线的长是 .
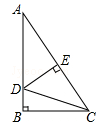
如图,,点
在边
上,
,点
为边
上一动点,连接
,△
与
关于
所在直线对称,点
,
分别为
,
的中点,连接
并延长交
所在直线于点
,连接
.当△
为直角三角形时,
的长为 .
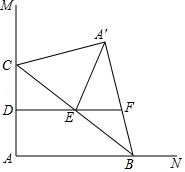
如图,在中,
,
.将
绕点
逆时针旋转一定角度后得到
,其中点
的对应点
落在边
上,则图中阴影部分的面积是 .

如图,在中,
,
,
.
是边
上任意一点,沿
剪开,将
沿
方向平移到
的位置,得到四边形
,则四边形
周长的最小值为 .

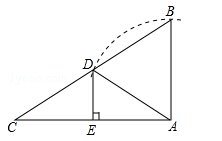
如图是一张长方形纸片 ,已知 , , 为 上一点, ,现要剪下一张等腰三角形纸片 ,使点 落在长方形 的某一条边上,则等腰三角形 的底边长是 .

如图,在矩形纸片中,
,
,点
在
上,将
沿
折叠,点
恰落在边
上的点
处;点
在
上,将
沿
折叠,点
恰落在线段
上的点
处,有下列结论:
①;②
;③
;④
.
其中正确的是 .(把所有正确结论的序号都选上)

如图,在Rt△ABC中,∠C=30°,以直角顶点A为圆心,AB长为半径画弧交BC于点D,过D作DE⊥AC于点E.若DE=a,则△ABC的周长用含a的代数式表示为__________.
(年贵州省黔东南州)如图,AD是⊙O的直径,弦BC⊥AD于E,AB=BC=12,则OC= .

(年贵州省贵阳市)“赵爽弦图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形(如图所示).小亮随机地向大正方形内部区域投飞镖.若直角三角形两条直角边的长分别是2和1,则飞镖投到小正方形(阴影)区域的概率是 .

(年云南省曲靖市)如图,在Rt△ABC中,∠C=30°,以直角顶点A为圆心,AB长为半径画弧交BC于点D,过D作DE⊥AC于点E.若DE=a,则△ABC的周长用含a的代数式表示为 .
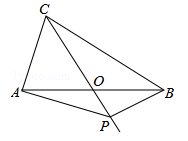
(年江西省南昌市)如图,在△ABC中,AB=BC=4,AO=BO,P是射线CO上的一个动点,∠AOC=60°,则当△PAB为直角三角形时,AP的长为 .
(年青海省西宁市)如图,Rt△ABC中,∠B=90°,AB=4,BC=3,AC的垂直平分线DE分别交AB,AC于D,E两点,则CD的长为 .