初中数学三角形三边关系试题

如图，在 $\text{Rt}\Delta \text{ABC}$中， $\angle \mathit{ACB}=90°$， $\mathit{AC}=8$， $\mathit{BC}=6$，点 $P$是平面内一个动点，且 $\mathit{AP}=3$， $Q$为 $\mathit{BP}$的中点，在 $P$点运动过程中，设线段 $\mathit{CQ}$的长度为 $m$，则 $m$的取值范围是 　　．

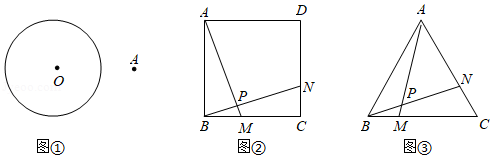
（1）如图①，点是外一点，点是上一动点．若的半径为3，且，则点到点的最短距离为　 ；

（2）如图②，已知正方形的边长为4，点、分别从点、同时出发，以相同的速度沿边、方向向终点和运动，连接和交于点，则点到点的最短距离为　　；

（3）如图③，在等边中，，点、分别从点、同时出发，以相同的速度沿边、方向向终点和运动，连接和交于点，求面积的最大值，并说明理由．

问题提出

（1）如图①，在 $\mathit{\Delta ABC}$ 中， $\mathit{BC}=6$ ， $D$ 为 $\mathit{BC}$ 上一点， $\mathit{AD}=4$ ，则 $\mathit{\Delta ABC}$ 面积的最大值是 　　．

问题探究

（2）如图②，已知矩形 $\mathit{ABCD}$ 的周长为12，求矩形 $\mathit{ABCD}$ 面积的最大值．

问题解决

（3）如图③， $\mathit{\Delta ABC}$ 是葛叔叔家的菜地示意图，其中 $\mathit{AB}=30$ 米， $\mathit{BC}=40$ 米， $\mathit{AC}=50$ 米，现在他想利用周边地的情况，把原来的三角形地拓展成符合条件的面积尽可能大、周长尽可能长的四边形地，用来建鱼塘．已知葛叔叔欲建的鱼塘是四边形 $\mathit{ABCD}$ ，且满足 $\angle \mathit{ADC}=60°$ ．你认为葛叔叔的想法能否实现？若能，求出这个四边形鱼塘周长的最大值；若不能，请说明理由．