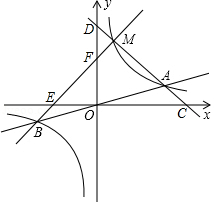
如图, , , , , 是直线 上的点,且 ,分别过点 , , , , 作 的垂线与直线 相交于点 , , , , ,连接 , , , , , ,交点依次为 , , , ,设△ ,△ ,△ , ,△ 的面积分别为 , , , ,则 .(用含有正整数 的式子表示)

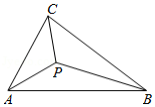
如图, 是 的内心,连接 、 、 , 、 、 的面积分别为 、 、 .则 .(填“ ”或“ ”或“ ”
如图, 中, , , , 为 边的中点,以 上一点 为圆心的 和 、 均相切,则 的半径为 .

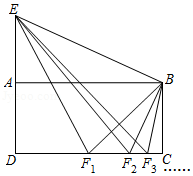
如图,四边形 是矩形,延长 到点 ,使 ,连接 ,点 是 的中点,连接 , ,得到△ ;点 是 的中点,连接 , ,得到△ ;点 是 的中点,连接 , ,得到△ ; ;按照此规律继续进行下去,若矩形 的面积等于2,则△ 的面积为 .(用含正整数 的式子表示)
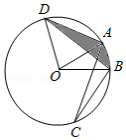
如图,点 , , 是 上的点,连接 , , ,且 ,过点 作 交 于点 ,连接 , ,已知 半径为2,则图中阴影面积为 .
如图,在 中, , ,以点 为圆心,线段 的长为半径作 ,交 的延长线于点 ,则阴影部分的面积为 (结果保留 .

如图,在 中,按以下步骤作图:
①以点 为圆心,任意长为半径作弧,分别交 、 于点 、 .
②分别以点 、 为圆心,大于 的同样长为半径作弧,两弧交于点 .
③作射线 交 于点 .
如果 , , 的面积为18,则 的面积为 .

如图,在平面直角坐标系中,半径为2的
与
轴的正半轴交于点
,点
是
上一动点,点
为弦
的中点,直线
与
轴、
轴分别交于点
、
,则
面积的最小值为 .

如图,正比例函数与反比例函数
的图象交于
,
两点,过点
作
轴于点
,过点
作
轴于点
,则
的面积为 .

如图①,已知正方体的棱长为
,
,
,
分别是
,
,
的中点,截面
将这个正方体切去一个角后得到一个新的几何体(如图②
,则图②中阴影部分的面积为
.

如图,函数为常数,
的图象与过原点的
的直线相交于
,
两点,点
是第一象限内双曲线上的动点(点
在点
的左侧),直线
分别交
轴,
轴于
,
两点,连接
分别交
轴,
轴于点
,
.现有以下四个结论:
①与
的面积相等;②若
于点
,则
;③若
点的横坐标为1,
为等边三角形,则
;④若
,则
.
其中正确的结论的序号是 .(只填序号)