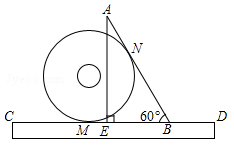
(年贵州省贵阳市)小明把半径为1的光盘、直尺和三角尺形状的纸片按如图所示放置于桌面上,此时,光盘与AB,CD分别相切于点N,M.现从如图所示的位置开始,将光盘在直尺边上沿着CD向右滚动到再次与AB相切时,光盘的圆心经过的距离是 .
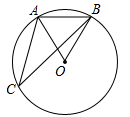
(年云南省)如图,点A,B,C是⊙O上的点,OA=AB,则∠C的度数为 .
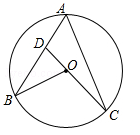
(年江西省南昌市)如图,点A,B,C在⊙O上,CO的延长线交AB于点D,∠A=50°,∠B=30°,则∠ADC的度数为 .
(年贵州省黔东南州)如图,AD是⊙O的直径,弦BC⊥AD于E,AB=BC=12,则OC= .

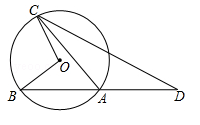
(年青海省中考)如图,点O为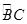 所在圆的圆心,∠BOC=112°,点D在BA的延长线上,AD=AC,则∠D= .
所在圆的圆心,∠BOC=112°,点D在BA的延长线上,AD=AC,则∠D= .
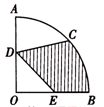
(年贵州省遵义市)如图,在圆心角为 的扇形OAB中,半径OA=2
的扇形OAB中,半径OA=2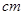 ,C为弧AB的中点,D,E分别是OA,OB的中点,则图中阴影部分的面积为
,C为弧AB的中点,D,E分别是OA,OB的中点,则图中阴影部分的面积为 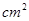 .
.
(年贵州省黔南州)如图,边长为1的菱形ABCD的两个顶点B、C恰好落在扇形AEF的弧EF上.若∠BAD=120°,则弧BC的长度等于 (结果保留π).
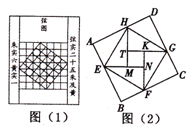
(年贵州省贵阳市)“赵爽弦图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形(如图所示).小亮随机地向大正方形内部区域投飞镖.若直角三角形两条直角边的长分别是2和1,则飞镖投到小正方形(阴影)区域的概率是 .

(年贵州省黔东南州)如图,在四边形ABCD中,AB∥CD,连接BD.请添加一个适当的条件 ,使△ABD≌△CDB.(只需写一个)

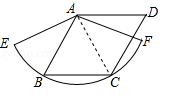
(年贵州省遵义市)我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”(如图(1)),图(2)由弦图变化得到,它是由八个全等的直角三角形拼接而成,记图中正方形ABCD、正方形EFGH、正方形MNKT的面积分别为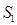 、
、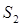 、
、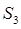 .若正方形EFGH的边长为2,则
.若正方形EFGH的边长为2,则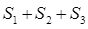 = .
= .
(年青海省中考)如图,点B,F,C,E在同一直线上,BF=CE,AB∥DE,请添加一个条件,使△ABC≌△DEF,这个添加的条件可以是 (只需写一个,不添加辅助线).

(年云南省曲靖市)如图,在Rt△ABC中,∠C=30°,以直角顶点A为圆心,AB长为半径画弧交BC于点D,过D作DE⊥AC于点E.若DE=a,则△ABC的周长用含a的代数式表示为 .
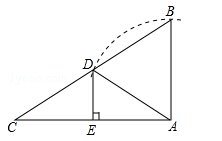
(年青海省西宁市)等腰三角形一腰上的高与另一腰的夹角的度数为20°,则顶角的度数是 .
(年青海省西宁市)如图,△ABC是边长为1的等边三角形,BD为AC边上的高,将△ABC折叠,使点B与点D重合,折痕EF交BD于点D1,再将△BEF折叠,使点B于点D1重合,折痕GH交BD1于点D2,依次折叠,则BDn= .

(年江西省南昌市)如图,OP平分∠MON,PE⊥OM于E,PF⊥ON于F,OA=OB,则图中有 对全等三角形.
