如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上一个动点,若PA=3,则PQ的最小值为( )

A. |
B.2 | C.3 | D.2 |
下列条件中,不能判断△ABC为直角三角形的是( )
| A.a2=1,b2=2,c2=3 |
| B.a:b:c=3:4:5 |
| C.∠A+∠B=∠C |
| D.∠A:∠B:∠C=3:4:5 |
如图为八个全等的正六边形(六条边相等,六个角相等)紧密排列在同一平面上的情形.根据图中标示的各点位置,下列三角形中与△ACD全等的是( )

| A.△ACF | B.△AED | C.△ABC | D.△BCF |
如图,已知AB=AC,∠A=36°,AB的中垂线MD交AC于点D,交AB于点M.下列结论:①BD是∠ABC的平分线;②△BCD是等腰三角形;③DC+BC=AB,正确的有( )
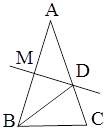
| A.3个 | B.2个 | C.1个 | D.0个 |
满足下列条件的△ABC不是直角三角形的是( )
A.BC=1,AC=2,AB=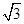 |
| B.BC:AC:AB=3:4:5 |
| C.∠A+∠B=∠C |
| D.∠A:∠B:∠C=3:4:5 |
如图,圆柱底面半径为 cm,高为9cm,点A、B分别是圆柱两底面圆周上的点,且A、B在同一母线上,用一根棉线从A点顺着圆柱侧面绕3圈到B点,则这根棉线的长度最短为( )
cm,高为9cm,点A、B分别是圆柱两底面圆周上的点,且A、B在同一母线上,用一根棉线从A点顺着圆柱侧面绕3圈到B点,则这根棉线的长度最短为( )

A.12cm B. cm C.15cm D.
cm C.15cm D. cm
cm
如下图,已知△ABE≌△ACD,∠1=∠2,∠B=∠C,不正确的等式是( )

| A.AB=AC | B.∠BAE=∠CAD | C.BE=DC | D.AD=DE |
如图是一个等边三角形木框,甲虫 在边框
在边框 上爬行(
上爬行( ,
, 端点除外),设甲虫
端点除外),设甲虫 到另外两边的距离之和为
到另外两边的距离之和为 ,等边三角形
,等边三角形 的高为
的高为 ,则
,则 与
与 的大小关系是( )
的大小关系是( )

A. |
B. |
C. |
D.无法确定 |
如图,在下列条件中,不能证明△ABD≌△ACD的条件是( )

| A.∠B=∠C,BD=DC |
| B.∠ADB=∠ADC,BD=DC |
| C.∠B=∠C,∠BAD=∠CAD |
| D.BD=DC,AB="AC" |
如图所示,一段楼梯的高BC是3m,斜边AC是5m,如果在楼梯上铺地毯,那么至少需要地毯( )

| A.5m | B.6m | C.7m | D.8m |
为了加快灾后重建的步伐,我市某镇要在三条公路围成的一块平地上修建一个砂石场,如图,要使这个砂石场到三条公路的距离相等,则可供选择的地址( )

| A.仅有一处 | B.有四处 | C.有七处 | D.有无数处 |
两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中AD=CD,AB=CB,小明在探究筝形的性质时,得到如下结论:

①AC⊥BD;②AO=CO= AC;③△ABD≌△CBD,其中正确的结论有( )
AC;③△ABD≌△CBD,其中正确的结论有( )
| A.①② | B.①③ | C.②③ | D.①②③ |
如图,已知AE=CF,∠AFD=∠CEB,那么添加下列一个条件后,仍无法判定△ADF≌△CBE的是( )

| A.AD=CB | B.∠A=∠C | C.BE=DF | D.AD//BC |