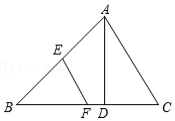
如图,在 中, , , 于点 , .若 , 分别为 , 的中点,则 的长为
| A. |
|
B. |
|
C. |
1 |
D. |
|
如图,在 中, , , 平分 交 于点 , ,垂足为 .若 ,则 的长为

| A. |
|
B. |
|
C. |
|
D. |
3 |
如图,在 中, , , 为 边上的中线, 平分 ,交 边于点 ,过点 作 ,垂足为 ,则 的度数为

| A. |
|
B. |
|
C. |
|
D. |
|
如图,在 中, 是 的垂直平分线,且分别交 , 于点 和 , , ,则 为

A. B. C. D.
如图,正方形 和正方形 的顶点 , , 在同一条直线上,顶点 , , 在同一条直线上. 是 的中点, 的平分线 过点 ,交 于点 ,连接 交 于点 ,连接 .以下四个结论:① ;② ;③ ;④ ,其中正确的结论是

A.①②③B.①②④C.①③④D.②③④
如图,把含 的直角三角板 放置在正方形 中, ,直角顶点 在正方形 的对角线 上,点 , 分别在 和 边上, 与 交于点 ,且点 为 的中点,则 的度数为

| A. |
|
B. |
|
C. |
|
D. |
|
如图,点 , , , 共线, , ,添加一个条件,不能判断 的是

| A. |
|
B. |
|
C. |
|
D. |
|
如图,在 纸片中, , , ,点 , 分别在 , 上,连结 ,将 沿 翻折,使点 的对应点 落在 的延长线上,若 平分 ,则 的长为

| A. |
|
B. |
|
C. |
|
D. |
|
如图是中国古代数学家赵爽用来证明勾股定理的弦图的示意图,它是由四个全等的直角三角形和一个小正方形 组成,恰好拼成一个大正方形 .连结 并延长交 于点 .若 , ,则 的长为

| A. |
|
B. |
|
C. |
|
D. |
|
如图,在矩形 中,点 在 上,将矩形沿 折叠,使点 落在 边上的点 处.若 , ,则 的值为

A. B. C. D.
如图,等边三角形 边长是定值,点 是它的外心,过点 任意作一条直线分别交 , 于点 , .将 沿直线 折叠,得到△ ,若 , 分别交 于点 , ,连接 , ,则下列判断错误的是

A.
B.△ 的周长是一个定值
C.四边形 的面积是一个定值
D.四边形 的面积是一个定值
如图,等腰 中,点 , 分别在腰 , 上,添加下列条件,不能判定 的是

A. B. C. D.