初中数学三角形试题

如图是由边长都是1的小正方形组成的网格．请以图中线段BC为边，作△PBC，使P在格点上，并满足：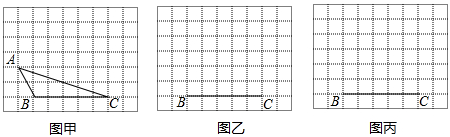

（1）图甲中的△PBC是直角三角形，且面积是△ABC面积2倍；
（2）图乙中的△PBC是等腰非直角三角形．

如图，△ABC的角平分线AD、BE交于点F，点F到边BC的距离为2cm，那么点F到边AC的距离为__________cm．

如图，在Rt△ABC中，∠C=30°，以直角顶点A为圆心，AB长为半径画弧交BC于点D，过D作DE⊥AC于点E．若DE=a，则△ABC的周长用含a的代数式表示为__________．

如图是一个等边三角形木框，甲虫在边框上爬行（，端点除外），设甲虫到另外两边的距离之和为，等边三角形的高为，则与的大小关系是（  ）

A．

B．

C．

D．无法确定

已知：如图，点在同一直线上，，，∥．求证：．

一长方体容器（如图1），长、宽均为2，高为8,里面盛有水，水面高为5，若沿底面一棱进行旋转倾斜，倾斜后的长方体容器的主视图如图2所示,若倾斜容器使水恰好倒出容器，则CD=         ．

如图，在四边形ABCD中，点E、F是BC、CD的中点，且AE⊥BC，AF⊥CD．

（1）求证：AB=AD．
（2）请你探究∠EAF，∠BAE，∠DAF之间有什么数量关系？并证明你的结论．

数学课上，探讨角平分线的作法时，李老师用直尺和圆规作角平分线，方法如下：

小颖的身边只有刻度尺，经过尝试，她发现利用刻度尺也可以作角平分线．
根据以上情境，解决下列问题：
①李老师用尺规作角平分线时，用到的三角形全等的判定方法是_________．
②小聪的作法正确吗？请说明理由．
③请你帮小颖设计用刻度尺作角平分线的方法．（要求：作出图形，写出作图步骤，不予证明）

两组邻边分别相等的四边形叫做“筝形”，如图，四边形ABCD是一个筝形，其中AD=CD，AB=CB，小明在探究筝形的性质时，得到如下结论：

①AC⊥BD；②AO=CO=AC；③△ABD≌△CBD，其中正确的结论有（  ）

A．①②

B．①③

C．②③

D．①②③

如图，点D是△ABC的边BC上任意一点，点E、F分别是线段AD、CE的中点，且△ABC的面积为16cm²，则△BEF的面积：            cm²．

如图，AB=AC，要使△ABE≌△ACD，依据ASA，应添加的一个条件是          ．

如图，在△ABC中，∠ACB=90°，分别以点A和B为圆心，以相同的长（大于AB）为半径作弧，两弧相交于点M和N，作直线MN交AB于点D，交BC于点E，连接CD，下列结论错误的是（  ）

A．AD=BD             B．CD=BD
C．∠A=∠BED         D．∠ECD=∠EDC

如图，已知D是BC的中点，过点D作BC的垂线交∠A的平分线于点E，EF⊥AB于点F，EG⊥AC于点G．求证：BF=CG．

如图，AE⊥AB，且AE=AB，BC⊥CD，且BC=CD，请按照图中所标注的数据计算图中实线所围成的图形的面积S= ___________．

已知D、E分别是△ABC的边BC和AC的中点，若△ABC的面积=36cm，则△DEC的面积为___________．