小光准备从 地去往 地,打开导航、显示两地距离为 ,但导航提供的三条可选路线长却分别为 , , (如图).能解释这一现象的数学知识是
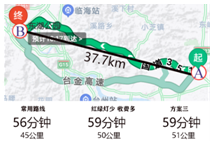
| A. |
两点之间,线段最短 |
B. |
垂线段最短 |
| C. |
三角形两边之和大于第三边 |
D. |
两点确定一条直线 |
某同学用剪刀沿直线将一片平整的银杏叶剪掉一部分(如图),发现剩下的银杏叶的周长比原银杏叶的周长要小,能正确解释这一现象的数学知识是

A.两点之间线段最短
B.两点确定一条直线
C.垂线段最短
D.经过直线外一点,有且只有一条直线与这条直线平行
如图,点 , 都在双曲线 上,点 , ,分别是 轴, 轴上的动点,则四边形 周长的最小值为
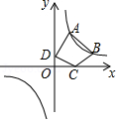
A. B. C. D.
如图,在 中, , , ,点 是 的三等分点,半圆 与 相切, , 分别是 与半圆弧上的动点,则 的最小值和最大值之和是
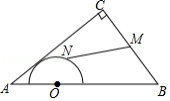
A.5B.6C.7D.8
对下列生活现象的解释其数学原理运用错误的是( )
A.把一条弯曲的道路改成直道可以缩短路程是运用了“两点之间线段最短”的原理
B.木匠师傅在刨平的木板上任选两个点就能画出一条笔直的墨线是运用了“直线外一点与直线上各点连接的所有线段中,垂线段最短”的原理
C.将自行车的车架设计为三角形形状是运用了“三角形的稳定性”的原理
D.将车轮设计为圆形是运用了“圆的旋转对称性”的原理
如图,田亮同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,能正确解释这一现象的数学知识是( )

A.垂线段最短
B.经过一点有无数条直线
C.经过两点,有且仅有一条直线
D.两点之间,线段最短
曲桥是我国古代经典建筑之一,它的修建增加了游人在桥上行走的路程,有利于游人更好地观赏风光.如图, 、 两地间修建曲桥与修建直的桥相比,增加了桥的长度,其中蕴含的数学道理是

| A. |
两点之间,线段最短 |
| B. |
平行于同一条直线的两条直线平行 |
| C. |
垂线段最短 |
| D. |
两点确定一条直线 |
下列叙述正确的是( )
| A. | 画直线AB=10厘米 |
| B. | 若AB=6,BC=2,那么AC=8或4 |
| C. | 河道改直可以缩短航程,是因为"经过两点有一条直线,并且只有一条直线" |
| D. | 在直线AB上任取4点,以这4点为端点的线段共有6条 |
下列说法中正确的是( )
| A.两点之间的所有连线中,线段最短 |
| B.射线就是直线 |
| C.两条射线组成的图形叫做角 |
| D.小于平角的角可分为锐角和钝角两类 |
如图,从A到B有①,②,③三条路线,最短的路线是①,其理由是( )

| A.因为它最直 |
| B.两点确定一条直线 |
| C.两点间的距离的概念 |
| D.两点之间,线段最短 |
“把弯曲的公路改直,就能缩短路程”,其中蕴含的数学道理是( )
| A.两点确定一条直线 |
| B.直线比曲线短 |
| C.两点之间线段最短 |
| D.两点之间直线最短 |
如图,从A地到B地走②路线最近,这样做的数学根据是( )
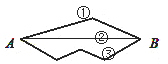
| A.两点确定一条直线 |
| B.两点之间,线段最短 |
| C.垂线段最短 |
| D.同位角相等,两直线平行 |