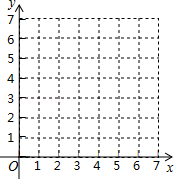
请用学过的方法研究一类新函数 为常数, 的图象和性质.
(1)在给出的平面直角坐标系中画出函数 的图象;
(2)对于函数 ,当自变量 的值增大时,函数值 怎样变化?
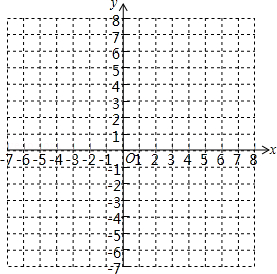
在 中, 边的长为 , 边上的高为 , 的面积为2.
(1) 关于 的函数关系式是 , 的取值范围是 ;
(2)在平面直角坐标系中画出该函数图象;
(3)将直线 向上平移 个单位长度后与上述函数图象有且只有一个交点,请求出此时 的值.
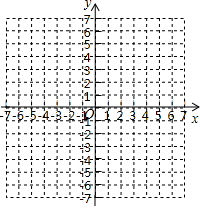
二次函数 的图象如图所示,则一次函数 和反比例函数 在同一平面直角坐标系中的图象可能是

A. B.
B.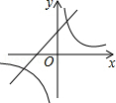
C. D.
D.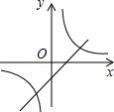
在同一直角坐标系中,函数 与 的大致图象是
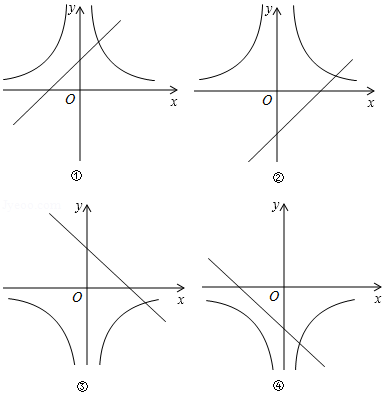
| A. |
①② |
B. |
②③ |
C. |
②④ |
D. |
③④ |
已知电流 (安培)、电压 (伏特)、电阻 (欧姆)之间的关系为 ,当电压为定值时, 关于 的函数图象是
A. B.
B.
C. D.
D.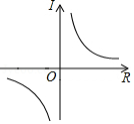
若二次函数 的图象如图所示,则一次函数 与反比例函数 在同一个坐标系内的大致图象为

| A. |
|
B. |
|
| C. |
|
D. |
|
如图为一次函数 与反比例函数 在同一坐标系中的大致图象,其中较准确的是
A. B.
B.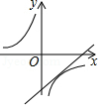
C.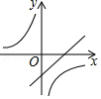 D.
D.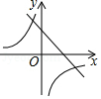
已知二次函数 的图象如图所示,则一次函数 的图象和反比例函数 的图象在同一坐标系中大致为
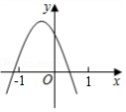
| A. |
|
B. |
|
| C. |
|
D. |
|
用数形结合等思想方法确定二次函数 的图象与反比例函数 的图象的交点的横坐标 所在的范围是
| A. |
|
B. |
|
C. |
|
D. |
|
经过实验获得两个变量 , 的一组对应值如下表.
|
1 |
2 |
3 |
4 |
5 |
6 |
|
6 |
2.9 |
2 |
1.5 |
1.2 |
1 |
(1)请画出相应函数的图象,并求出函数表达式.
(2)点 , , , 在此函数图象上.若 ,则 , 有怎样的大小关系?请说明理由.