如图,点 在直线 上,过点 作 轴的平行线交直线 于点 ,过点 作 的垂线交 于点 ,过点 作 轴的平行线交直线 于点 ,过点 作 的垂线交 于点 ,过点 作 轴的平行线交直线 于点 , ,过点 , , , ,分别作 的平行线交 于点 ,交 于点 ,交 于点 , ,按此规律继续下去,若 ,则点 的坐标为 .(用含正整数 的式子表示)

如图,在平面直角坐标系中,直线 与直线 相交于点 ,并分别与 轴相交于点 、 .
(1)求交点 的坐标;
(2)求 的面积;
(3)请把图象中直线 在直线 上方的部分描黑加粗,并写出此时自变量 的取值范围.
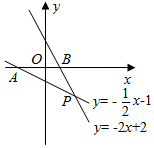
对于实数 , ,定义符号 , ,其意义为:当 时, , ;当 时, , .例如: , ,若关于 的函数 , ,则该函数的最大值为
A. B.1C. D.
如图,正比例函数 是常数, 的图象与一次函数 的图象相交于点 ,点 的纵坐标是2,则不等式 的解集是
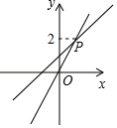
A. B. C. D.
数形结合是解决数学问题常用的思想方法.如图,直线 和直线 相交于点 ,根据图象可知,方程 的解是
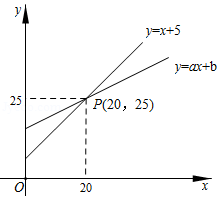
A. B. C. D.
在平面直角坐标系中, 为坐标原点.若直线 分别与 轴、直线 交于点 、 ,则 的面积为
A.2B.3C.4D.6