函数图象是研究函数的重要工具。探究函数性质时,我们经历了列表、描点、连线画出函数图象,然后观察分析图象特征,概括函数性质的过程。请结合已有的学习经验,画出函数 的图象,并探究其性质.
列表如下:
|
|
|
|
|
|
|
0 |
1 |
2 |
3 |
4 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
(1)写出表中 、 的值,并在平面直角坐标系中画出该函数的图象;
(2)观察函数 的图象,判断下列关于该函数性质的命题:
①当 时,函数图象关于直线 对称;
② 时,函数有最小值,最小值为 ;
③ 时,函数 的值随 的增大而减小.
其中正确的是 .(请写出所有正确命题的番号)
(3)结合图象,请写出不等式 的解集 .

下表中列出的是一个二次函数的自变量 与函数 的几组对应值:
|
|
|
|
0 |
1 |
3 |
|
|
|
|
6 |
|
|
|
|
下列各选项中,正确的是
| A. |
这个函数的图象开口向下 |
| B. |
这个函数的图象与 轴无交点 |
| C. |
这个函数的最小值小于 |
| D. |
当 时, 的值随 值的增大而增大 |
如图1,在 中, , , ,点D为AB的中点,线段 上有一动点E,连接DE,作DA关于直线DE的对称图形,得到 ,过点F作 于点G.设A、E两点间的距离为 , 两点间的距离为
小军根据学习函数的经验,对因变量y随自变量x的变化而变化的规律进行了探究.
下面是小军的探究过程,请补充完整.

(1)列表:如表的已知数据是根据A,E两点间的距离x进行取点、画图、测量,分别得到了x与y的几组对应值:
x/cm |
0 |
0.51 |
1.03 |
1.41 |
1.50 |
1.75 |
2.20 |
2.68 |
3.00 |
3.61 |
4.10 |
4.74 |
5.00 |
y/cm |
0 |
0.94 |
1.91 |
2.49 |
|
2.84 |
3.00 |
2.84 |
2.60 |
2.00 |
1.50 |
0.90 |
0.68 |
请你通过计算补全表格;
(2)描点、连线:在平面直角坐标系 中(如图2),描出表中各组数值所对应的点 ,并画出y关于x的图象;
(3)探究性质:随着x值的不断增大,y的值是怎样变化的? ;
(4)解决问题:当 时,FG的长度大约是 cm(保留两位小数).
下表中 与 的数据满足我们初中学过的某种函数关系.其函数表达式为 .
|
|
|
0 |
1 |
3 |
|
|
|
0 |
3 |
4 |
0 |
|
已知甲、乙两个函数图象上部分点的横坐标 与对应的纵坐标
与对应的纵坐标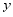 分别如表所示,两个函数图象仅有一个交点,则交点的纵坐标
分别如表所示,两个函数图象仅有一个交点,则交点的纵坐标 是
是
甲
|
1 |
2 |
3 |
4 |
|
0 |
1 |
2 |
3 |
乙
|
|
2 |
4 |
6 |
|
0 |
2 |
3 |
4 |
A.0B.1C.2D.3