初中数学坐标确定位置试题

一个不透明的袋子中装有四个小球，上面分别标有数字，，0，1，它们除了数字不同外，其它完全相同．

（1）随机从袋子中摸出一个小球，摸出的球上面标的数字为正数的概率是　　．

（2）小聪先从袋子中随机摸出一个小球，记下数字作为平面直角坐标系内点的横坐标；然后放回搅匀，接着小明从袋子中随机摸出一个小球，记下数字作为点的纵坐标．如图，已知四边形的四个顶点的坐标分别为，，，，请用画树状图或列表法，求点落在四边形所围成的部分内（含边界）的概率．

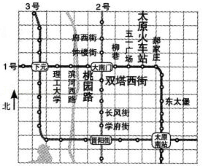
如图是利用网格画出的太原市地铁1，2，3号线路部分规划示意图，若建立适当的平面直角坐标系，表示双塔西街点的坐标为，表示桃园路的点的坐标为，则表示太原火车站的点（正好在网格点上）的坐标是　　．

如图所示，小球从台球桌面 $\mathit{ABCO}$ 上的点 $P(0,1)$ 出发，撞击桌边发生反弹，反射角等于入射角若小球以每秒 $\sqrt{2}$ 个单位长度的速度沿图中箭头方向运动，则第50秒的小球所在位置的坐标为 $($ 　　 $)$

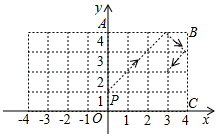
A．

$(2,3)$

B．

$(3,4)$

C．

$(3,2)$

D．

$(0,1)$

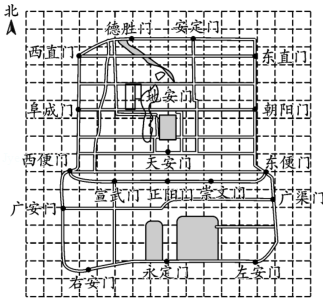
如图是老北京城一些地点的分布示意图．在图中，分别以正东、正北方向为 $x$ 轴、 $y$ 轴的正方向建立平面直角坐标系，有如下四个结论：

①当表示天安门的点的坐标为 $(0,0)$ ，表示广安门的点的坐标为 $(-6,-3)$ 时，表示左安门的点的坐标为 $(5,-6)$ ；

②当表示天安门的点的坐标为 $(0,0)$ ，表示广安门的点的坐标为 $(-12,-6)$ 时，表示左安门的点的坐标为 $(10,-12)$ ；

③当表示天安门的点的坐标为 $(1,1)$ ，表示广安门的点的坐标为 $(-11,-5)$ 时，表示左安门的点的坐标为 $(11,-11)$ ；

④当表示天安门的点的坐标为 $(1.5,1.5)$ ，表示广安门的点的坐标为 $(-16.5,-7.5)$ 时，表示左安门的点的坐标为 $(16.5,-16.5)$ ．

上述结论中，所有正确结论的序号是 $($ 　　 $)$

A．

①②③

B．

②③④

C．

①④

D．

①②③④

如图，一只甲虫在5×5的方格（每小格边长为1）上沿着网格线运动。它从A处出发去看望B、C、D处的其它甲虫，规定：向上向右走为正，向下向左走为负。如果从A到B记为：A→B（+1，+3）；从C到D记为：C→D（+1，－2）。其中第一个数表示左右方向，第二个数表示上下方向，那么图中

（1）A→C（   ，   ），C→（-2，   ）；
（2）若这只甲虫的行走路线为A→B→C→D，请计算该甲虫走过的路程；
（3）假如这只甲虫从A处去甲虫P处的行走路线依次为
（＋2，＋2），（＋1，－1），（－2，＋3），请在图中标出P的位置．

将正整数从1开始，按如图所表示的规律排列．规定图中第m行、第n列的位置记作（m，n），如正整数8的位置是（2，3），则正整数137的位置记作          ．

（年江西省南昌市）如图，正方形ABCD于正方形A₁B₁C₁D₁关于某点中心对称，已知A，D₁，D三点的坐标分别是（0，4），（0，3），（0，2）．

（1）求对称中心的坐标；
（2）写出顶点B，C，B₁，C₁的坐标．

初三年级某班有54名学生，所在教室有6行9列座位，用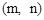表示第行第列的座位，新学期准备调整座位，设某个学生原来的座位为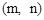，如果调整后的座位为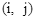，则称该生作了平移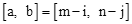,并称为该生的位置数。若当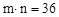时，取得最小值，则该生位置数的最大值为        。

如图，在平面直角坐标系中， $\mathit{\Delta AOB}$的边 $\mathit{OA}$在 $x$轴上， $\mathit{OA}=\mathit{AB}$，且线段 $\mathit{OA}$的长是方程 $x^2-4x-5=0$的根，过点 $B$作 $\mathit{BE}\perp x$轴，垂足为 $E$， $\tan \angle \mathit{BAE}=\frac{4}{3}$，动点 $M$以每秒1个单位长度的速度，从点 $A$出发，沿线段 $\mathit{AB}$向点 $B$运动，到达点 $B$停止．过点 $M$作 $x$轴的垂线，垂足为 $D$，以 $\mathit{MD}$为边作正方形 $\mathit{MDCF}$，点 $C$在线段 $\mathit{OA}$上，设正方形 $\mathit{MDCF}$与 $\mathit{\Delta AOB}$重叠部分的面积为 $S$，点 $M$的运动时间为 $t(t>0)$秒．

（1）求点 $B$的坐标；

（2）求 $S$关于 $t$的函数关系式，并写出自变量 $t$的取值范围；

（3）当点 $F$落在线段 $\mathit{OB}$上时，坐标平面内是否存在一点 $P$，使以 $M$、 $A$、 $O$、 $P$为顶点的四边形是平行四边形？若存在，直接写出点 $P$的坐标；若不存在，请说明理由．