初中数学坐标确定位置试题

在电影院中，若将电影票上“8排6号”记作（8，6），那么“5排4号”应记作___________．

如图是一局围棋比赛的几手棋.为记录棋谱方便，横线用数字表示，纵线用字母表示，这样，黑棋的位置可记为（B,2），白棋②的位置可记为（D,1），则白棋⑨的位置应记为（  ）

A．（C，5）        B．（C，4）        C．（4，C）         D．（5，C）

下图是轰炸机群一个飞行队形，如果最后两架轰炸机的平面坐标分别是A（-2，1）和B（-2，-3），那么第一架轰炸机C的平面坐标是            .

如图是一片枫叶标本，其形状呈"掌状五裂型"，裂片具有少数突出的齿，将其放在平面直角坐标系中，表示叶片"顶部" $A$ ， $B$ 两点的坐标分别为 $(-2,2)$ ， $(-3,0)$ ，则叶杆"底部"点 $C$ 的坐标为 　　．

如图是学校与小明家位置示意图，如果以学校所在位置为坐标原点，水平方向为x轴建立直角坐标系，那么小明家所在位置的坐标为__________．

定义：在平面直角坐标系 $\mathit{xOy}$中，把从点 $P$出发沿纵或横方向到达点 $Q$（至多拐一次弯）的路径长称为 $P$， $Q$的“实际距离”．如图，若 $P(-1,1)$， $Q(2,3)$，则 $P$， $Q$的“实际距离”为5，即 $\mathit{PS}+\mathit{SQ}=5$或 $\mathit{PT}+\mathit{TQ}=5$．环保低碳的共享单车，正式成为市民出行喜欢的交通工具．设 $A$， $B$， $C$三个小区的坐标分别为 $A(3,1)$， $B(5,-3)$， $C(-1,-5)$，若点 $M$表示单车停放点，且满足 $M$到 $A$， $B$， $C$的“实际距离”相等，则点 $M$的坐标为　　．

小明为画一个零件的轴截面，以该轴截面底边所在的直线为 $x$轴，对称轴为 $y$轴，建立如图所示的平面直角坐标系．若坐标轴的单位长度取 $1\mathit{mm}$，则图中转折点 $P$的坐标表示正确的是 $($　　 $)$

A． $(5,30)$B． $(8,10)$C． $(9,10)$D． $(10,10)$

在平面直角坐标系中，点 $(1,5)$所在的象限是 $($　　 $)$

A．第一象限B．第二象限C．第三象限D．第四象限

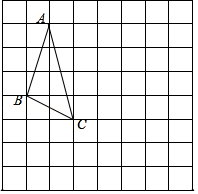
在下面的网格中，每个小正方形的边长均为1， $\mathit{\Delta ABC}$的三个顶点都是网格线的交点，已知 $B$， $C$两点的坐标分别为 $(-3,0)$， $(-1,-1)$．

（1）请在图中画出平面直角坐标系，并直接写出点 $A$的坐标．

（2）将 $\mathit{\Delta ABC}$绕着坐标原点顺时针旋转 $90°$，画出旋转后的△ $A\text{'}{B}^{\text{'}}C\text{'}$．

（3）接写出在上述旋转过程中，点 $A$所经过的路径长．

如图，在中国象棋的残局上建立平面直角坐标系，如果“相”和“兵”的坐标分别是 $(3,-1)$和 $(-3,1)$，那么“卒”的坐标为　　．

以水平数轴的原点为圆心，过正半轴上的每一刻度点画同心圆，将逆时针依次旋转、、、、得到11条射线，构成如图所示的“圆”坐标系，点、的坐标分别表示为、，则点的坐标表示为　   　．

小李、小王、小张、小谢原有位置如图（横为排、竖为列），小李在第2排第4列，小

王在第3排第3列，小张在第4排第2列，小谢在第5排第4列．撤走第一排，仍按照原有确定位置的方法确定新的位置，下列说法正确的是 $($ 　　 $)$

A．	小李现在位置为第1排第2列	B．	小张现在位置为第3排第2列
C．	小王现在位置为第2排第2列	D．	小谢现在位置为第4排第2列

如图， $\mathit{\Delta ABC}$外接圆的圆心坐标是　　．

一个不透明的袋子中装有四个小球，上面分别标有数字，，0，1，它们除了数字不同外，其它完全相同．

（1）随机从袋子中摸出一个小球，摸出的球上面标的数字为正数的概率是　　．

（2）小聪先从袋子中随机摸出一个小球，记下数字作为平面直角坐标系内点的横坐标；然后放回搅匀，接着小明从袋子中随机摸出一个小球，记下数字作为点的纵坐标．如图，已知四边形的四个顶点的坐标分别为，，，，请用画树状图或列表法，求点落在四边形所围成的部分内（含边界）的概率．

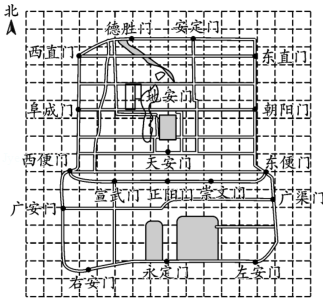
如图是老北京城一些地点的分布示意图．在图中，分别以正东、正北方向为 $x$ 轴、 $y$ 轴的正方向建立平面直角坐标系，有如下四个结论：

①当表示天安门的点的坐标为 $(0,0)$ ，表示广安门的点的坐标为 $(-6,-3)$ 时，表示左安门的点的坐标为 $(5,-6)$ ；

②当表示天安门的点的坐标为 $(0,0)$ ，表示广安门的点的坐标为 $(-12,-6)$ 时，表示左安门的点的坐标为 $(10,-12)$ ；

③当表示天安门的点的坐标为 $(1,1)$ ，表示广安门的点的坐标为 $(-11,-5)$ 时，表示左安门的点的坐标为 $(11,-11)$ ；

④当表示天安门的点的坐标为 $(1.5,1.5)$ ，表示广安门的点的坐标为 $(-16.5,-7.5)$ 时，表示左安门的点的坐标为 $(16.5,-16.5)$ ．

上述结论中，所有正确结论的序号是 $($ 　　 $)$

A．

①②③

B．

②③④

C．

①④

D．

①②③④