初中数学坐标确定位置试题

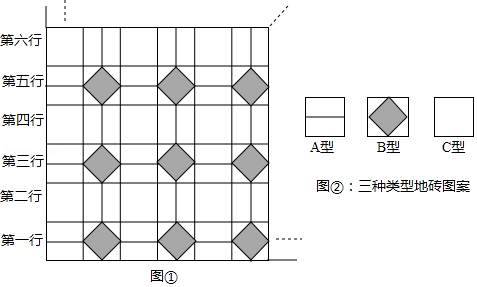
如图①，某广场地面是用 $A$， $B$， $C$三种类型地砖平铺而成的．三种类型地砖上表面图案如图②所示．现用有序数对表示每一块地砖的位置：第一行的第一块 $(A$型）地砖记作 $(1,1)$，第二块 $(B$型）地砖记作 $(2,1)\dots$若 $(m,n)$位置恰好为 $A$型地砖，则正整数 $m$， $n$须满足的条件是　        　．

小明为画一个零件的轴截面，以该轴截面底边所在的直线为 $x$轴，对称轴为 $y$轴，建立如图所示的平面直角坐标系．若坐标轴的单位长度取 $1\mathit{mm}$，则图中转折点 $P$的坐标表示正确的是 $($　　 $)$

A． $(5,30)$B． $(8,10)$C． $(9,10)$D． $(10,10)$

如图，在中国象棋的残局上建立平面直角坐标系，如果“相”和“兵”的坐标分别是 $(3,-1)$和 $(-3,1)$，那么“卒”的坐标为　　．

如图， $\mathit{\Delta ABC}$外接圆的圆心坐标是　　．

如图，在平面直角坐标系中，直线 $l$的函数表达式为 $y=x$，点 $O_1$的坐标为 $(1,0)$，以 $O_1$为圆心， $O_{1}O$为半径画圆，交直线 $l$于点 $P_1$，交 $x$轴正半轴于点 $O_2$，以 $O_2$为圆心， $O_{2}O$为半径画圆，交直线 $l$于点 $P_2$，交 $x$轴正半轴于点 $O_3$，以 $O_3$为圆心， $O_{3}O$为半径画圆，交直线 $l$于点 $P_3$，交 $x$轴正半轴于点 $O_4$； $\dots$按此做法进行下去，其中 $\stackrel{̂}{P_{2017}{O}_{2018}}$的长为　　．

定义：在平面直角坐标系 $\mathit{xOy}$中，把从点 $P$出发沿纵或横方向到达点 $Q$（至多拐一次弯）的路径长称为 $P$， $Q$的“实际距离”．如图，若 $P(-1,1)$， $Q(2,3)$，则 $P$， $Q$的“实际距离”为5，即 $\mathit{PS}+\mathit{SQ}=5$或 $\mathit{PT}+\mathit{TQ}=5$．环保低碳的共享单车，正式成为市民出行喜欢的交通工具．设 $A$， $B$， $C$三个小区的坐标分别为 $A(3,1)$， $B(5,-3)$， $C(-1,-5)$，若点 $M$表示单车停放点，且满足 $M$到 $A$， $B$， $C$的“实际距离”相等，则点 $M$的坐标为　　．

在平面直角坐标系中，点 $(1,5)$所在的象限是 $($　　 $)$

A．第一象限B．第二象限C．第三象限D．第四象限

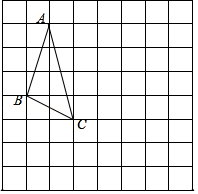
在下面的网格中，每个小正方形的边长均为1， $\mathit{\Delta ABC}$的三个顶点都是网格线的交点，已知 $B$， $C$两点的坐标分别为 $(-3,0)$， $(-1,-1)$．

（1）请在图中画出平面直角坐标系，并直接写出点 $A$的坐标．

（2）将 $\mathit{\Delta ABC}$绕着坐标原点顺时针旋转 $90°$，画出旋转后的△ $A\text{'}{B}^{\text{'}}C\text{'}$．

（3）接写出在上述旋转过程中，点 $A$所经过的路径长．

以水平数轴的原点为圆心，过正半轴上的每一刻度点画同心圆，将逆时针依次旋转、、、、得到11条射线，构成如图所示的“圆”坐标系，点、的坐标分别表示为、，则点的坐标表示为　   　．

小李、小王、小张、小谢原有位置如图（横为排、竖为列），小李在第2排第4列，小

王在第3排第3列，小张在第4排第2列，小谢在第5排第4列．撤走第一排，仍按照原有确定位置的方法确定新的位置，下列说法正确的是 $($ 　　 $)$

A．	小李现在位置为第1排第2列	B．	小张现在位置为第3排第2列
C．	小王现在位置为第2排第2列	D．	小谢现在位置为第4排第2列

一个不透明的袋子中装有四个小球，上面分别标有数字，，0，1，它们除了数字不同外，其它完全相同．

（1）随机从袋子中摸出一个小球，摸出的球上面标的数字为正数的概率是　　．

（2）小聪先从袋子中随机摸出一个小球，记下数字作为平面直角坐标系内点的横坐标；然后放回搅匀，接着小明从袋子中随机摸出一个小球，记下数字作为点的纵坐标．如图，已知四边形的四个顶点的坐标分别为，，，，请用画树状图或列表法，求点落在四边形所围成的部分内（含边界）的概率．

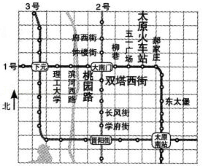
如图是利用网格画出的太原市地铁1，2，3号线路部分规划示意图，若建立适当的平面直角坐标系，表示双塔西街点的坐标为，表示桃园路的点的坐标为，则表示太原火车站的点（正好在网格点上）的坐标是　　．

如图所示，小球从台球桌面 $\mathit{ABCO}$ 上的点 $P(0,1)$ 出发，撞击桌边发生反弹，反射角等于入射角若小球以每秒 $\sqrt{2}$ 个单位长度的速度沿图中箭头方向运动，则第50秒的小球所在位置的坐标为 $($ 　　 $)$

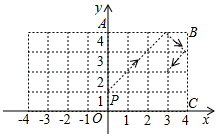
A．

$(2,3)$

B．

$(3,4)$

C．

$(3,2)$

D．

$(0,1)$

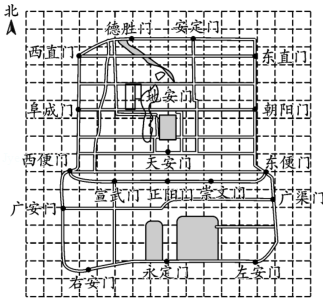
如图是老北京城一些地点的分布示意图．在图中，分别以正东、正北方向为 $x$ 轴、 $y$ 轴的正方向建立平面直角坐标系，有如下四个结论：

①当表示天安门的点的坐标为 $(0,0)$ ，表示广安门的点的坐标为 $(-6,-3)$ 时，表示左安门的点的坐标为 $(5,-6)$ ；

②当表示天安门的点的坐标为 $(0,0)$ ，表示广安门的点的坐标为 $(-12,-6)$ 时，表示左安门的点的坐标为 $(10,-12)$ ；

③当表示天安门的点的坐标为 $(1,1)$ ，表示广安门的点的坐标为 $(-11,-5)$ 时，表示左安门的点的坐标为 $(11,-11)$ ；

④当表示天安门的点的坐标为 $(1.5,1.5)$ ，表示广安门的点的坐标为 $(-16.5,-7.5)$ 时，表示左安门的点的坐标为 $(16.5,-16.5)$ ．

上述结论中，所有正确结论的序号是 $($ 　　 $)$

A．

①②③

B．

②③④

C．

①④

D．

①②③④

如图，一只甲虫在5×5的方格（每小格边长为1）上沿着网格线运动。它从A处出发去看望B、C、D处的其它甲虫，规定：向上向右走为正，向下向左走为负。如果从A到B记为：A→B（+1，+3）；从C到D记为：C→D（+1，－2）。其中第一个数表示左右方向，第二个数表示上下方向，那么图中

（1）A→C（   ，   ），C→（-2，   ）；
（2）若这只甲虫的行走路线为A→B→C→D，请计算该甲虫走过的路程；
（3）假如这只甲虫从A处去甲虫P处的行走路线依次为
（＋2，＋2），（＋1，－1），（－2，＋3），请在图中标出P的位置．